Parallèle entre test statistique et test diagnostique

1 Introduction

Il est possible d’établir un parallèle entre les tests statistiques réalisés à la recherche de l’effet du traitement dans un essai thérapeutique et les tests diagnostiques utilisés pour poser le diagnostique d’une maladie (1). Ce parallèle permet d’appréhender ce qu’est la valeur prédictive d’un résultat d’essai significatif. Cette façon de voir les tests statistiques introduit aussi l’approche Bayesienne (cf. ci-dessous).

L’hypothèse nulle (H0) d’inexistence de l’effet du traitement peut être assimilée à l’absence de la maladie (noté M-), tandis que l’hypothèse alternative (H1) d’existence de l’effet est à mettre en parallèle avec la présence de la maladie (M+).

Le résultat de l’essai, significatif (R+) ou non significatif (R-), est assimilable à l’existence ou non du signe (recherché par le test diagnostic). Le signe recherché est présent (S+) quand l’essai obtient un résultat significatif, le signe est absent (S-) en cas de résultat non significatif.

Le risque α est la probabilité d’obtenir un résultat significatif sous l’hypothèse nulle, c’est-à-dire la probabilité de présence du signe en l’absence de la maladie : . a est donc égal à où Sp désigne la spécificité du test (Sp=Pr(S-/M-)).

Le risque b est la probabilité de ne pas conclure, c’est-à-dire d’obtenir un résultat non significatif sous l’hypothèse alternative. Il correspond donc à la probabilité d’absence du signe en cas de maladie = Pr(S-/M+), b est donc égal à 1-Se où Se désigne la sensibilité (Se=Pr(S+/M+)). La puissance statistique W=1-β d’un essai est donc assimilable à la sensibilité d’un test diagnostique (détecter un effet lorsqu’il existe ou détecter un signe quand la maladie est présente).

Tableau 1 : Parallèle entre les table 2x2 du test diagnostic et du test d’hypothèse

	M+	M-		H1	H0
S+	Se	1-Sp	R+	1-β	α
S-	1-Se	Sp	R-	β	1- α

Avec un test diagnostique, la valeur prédictive positive (VPP) est la probabilité de la maladie lorsque l’on est en présence du signe. C’est la probabilité de la maladie a posteriori, lorsque l’on a connaissance du résultat du test diagnostique. La VPP dépend de la probabilité a priori de la maladie v. Au niveau du test statistique d’un essai, la VPP correspond à la probabilité de l’existence de l’effet du traitement lorsque l’essai a obtenu un résultat significatif. Ainsi :

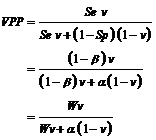
Cette formule est identique à celle obtenue en raisonnant avec les risques statistiques vus comme des taux de filtration (cf. chapitre principe général du test statistique). La probabilité a priori v est une notion difficile à cerner avec précision. Il s’agit plutôt d’une probabilité subjective, d’une sorte de degré de croyance en l’existence de l’efficacité du traitement avant de l’évaluer. En moyenne, cette probabilité a priori peut être assimilée à la fréquence moyenne des résultats positifs obtenus avec les essais thérapeutiques.

Ce développement est identique à celui que nous avons fait avec les risques statistiques vus comme des taux de filtration.

Le tableau 3 donne la probabilité de l’existence de l’effet du traitement après avoir obtenu un résultat significatif dans un essai en fonction du seuil de signification statistique, de la puissance statistique de l’essai W et de la probabilité a priori d’existence de l’effet du traitement (v).

Ainsi un résultat significatif n’a pas la même valeur (prédictive de l’effet du traitement) quand la probabilité a priori est faible ou forte. Dans des situations très spéculatives où l’essai est réalisé sans qu’il y ait de justification, la probabilité a priori est très faible. Dans ce cas, un essai significatif n’a pas beaucoup de valeur prédictive, même en cas de résultats hautement significatifs.

Tableau 2 – Parallèle entre test statistique d’un essai et test diagnostique

Test statistique

Test diagnostique

Absence d’effet

hypothèse nulle H0

Absence de la maladie

M-

Existence de l’effet

hypothèse alternative H1

Existence de la maladie

M+

Résultat de l’essai significatif

R+

Présence du signe recherché par le test diagnostique

S+

Résultat non significatif

R-

Absence du signe

S-

Risque alpha (ou valeur de p)

Pr(R+/H0)

Pr(S+/M-)=1-Pr(S-/M-)

=1-Sp (Sp=spécificité)

Risque beta

Pr(R-/H1)

Pr(S-/M+)=1-Pr(S+/M+)

=1-Se (Se= sensibilité)

Puissance W=1-β

Pr(R+/H1)

Se (sensiblité)

Pr(S+/M+)

Probabilité que le traitement soit efficace si le résultat est significatif

Valeur prédictive positive

P(M+/S+) = VPP

Probabilité a priori que l’hypothèse testée soit vraie

Probabilité a priori de la maladie

Avec les traitements médicamenteux, les essais d’efficacité (phase 3) sont entrepris après les essais de pharmacologie animale et les essais de phase 1 et 2. La probabilité a priori d’existence d’un effet est alors forte. Environ 5 à 10% des essais de phase 3 n’obtiennent pas de résultats significatifs. Avant essai, il est possible de dire, qu’en moyenne, la probabilité qu’un traitement issu des phases précédentes soit efficace est d’au moins 90%. La valeur prédictive d’un résultat significatif est alors importante.

La valeur prédictive d’un résultat significatif dépend aussi de la puissance de l’essai : elle est moins importante avec un essai de faible puissance qu’avec une étude dont la puissance statistique est élevée. La probabilité d’avoir à faire à un résultat faux positif (probabilité qui est 1-VPP) est d’autant plus importante que la puissance de l’essai est faible. Un résultat faux positif étant un résultat statistiquement significatif mais obtenu avec un traitement inefficace.

Tableau 3 – Probabilité de l’existence de l’effet du traitement après avoir obtenu un résultat significatif dans un essai en fonction du seuil de risque alpha, de la puissance statistique de l’essai W et de la probabilité a priori d’existence de l’effet du traitement (v).

W	Alpha
W	0.05	0.01	0.001
Probabilité a priori d’existence de l’effet v=90%
20%	97.3%	99.4%	99.9%
50%	98.9%	99.8%	100.0%
80%	99.3%	99.9%	100.0%
Probabilité a priori d’existence de l’effet v=50%
20%	80.0%	95.2%	99.5%
50%	90.9%	98.0%	99.8%
80%	94.1%	98.8%	99.9%
Probabilité a priori d’existence de l’effet v=10%
20%	30.8%	69.0%	95.7%
50%	52.6%	84.7%	98.2%
80%	64.0%	89.9%	98.9%
Probabilité a priori d’existence de l’effet v=1%
20%	3.9%	16.8%	66.9%
50%	9.2%	33.6%	83.5%
80%	13.9%	44.7%	89.0%

La fragilité possible de certaines preuves, issues pourtant d’un résultat statistiquement significatif, que laissent entr’apercevoir certaines valeurs de VPP du tableau 3, provient simplement du fait que les preuves disponibles en médecine sont parfois insuffisamment puissantes et concluantes. Cette approche rejoint les constatations que l’on peut être amené à faire avec l’analyse de la pertinence clinique des intervalles de confiance.

Si les preuves apportées par les essais peuvent paraître fragiles dans certains cas (car obtenues avec un faible degré de signification statistique et dans une petite étude peu puissante), c’est parce que les études réalisées sont trop petites ou insuffisamment justifiées.

2 A priori neutre

Le choix de la probabilité a priori est le maillon faible de cette approche. Sa détermination est constamment entachée de subjectivité. Ainsi il peut être considéré comme gênant que la valeur d’un résultat recueilli de façon rigoureuse, au prix de nombreux efforts soit ensuite malaxée avec un « a priori » très subjectif. Pour contourner cette difficulté, il est possible de prendre un « a priori » totalement neutre (on dit non informatif), correspondant à v=50%. On ne favorise, a priori, aucune hypothèse et on laisse les données décider entièrement de la conclusion. Dans ce cas, cette approche Bayesienne (cf. ci-dessous ) revient à l’approche fréquentiste simple. La VPP d’un résultat significatif au seuil de 5% sera égal à 95% (avec une étude puissante où la puissance est de 95%).

3 Approche fréquentiste, approche Bayesienne

Deux courants de pensée coexistent dans les statistiques inférentielles : l’approche fréquentiste et l’approche Bayesienne.

L’approche Bayesienne (2) est celle que nous venons de voir en faisant ce parallèle entre test statistique dans un essai et test diagnostique.

L’approche fréquentiste est l’utilisation simple des tests statistiques, sans chercher à exprimer la probabilité de l’hypothèse en fonction du résultat (probabilité a posteriori). C’est l’approche classique des tests statistiques. Cependant le résultat qu’elle produit, la probabilité d’observer les données sous l’hypothèse nulle, peut apparaître insatisfaisant, car ne répondant pas directement à la question que l’on se pose : qu’elle la probabilité que le traitement soit efficace.

Approche fréquentiste

Approche Bayesienne

Information apportée

Pr(résultat observé/H0)

P value

Pr(H1/résultat)

Valeur prédictive

L’approche Bayesienne cherche à estimer la probabilité de la conclusion, c’est-à-dire la probabilité de l’hypothèse alternative (probabilité a posteriori). En cherchant à estimer la probabilité a posteriori de l’hypothèse, l’approche Bayesienne nécessite l’introduction de la probabilité a priori. La probabilité a priori est difficile à obtenir. Elle ne provient pas, le plus souvent, de données mais d’une appréciation subjective. À ce niveau, se situe la principale difficulté et le point de faiblesse de cette approche. En effet, à partir du même essai, il va être possible de faire des conclusions parfois opposées en fonction de l’ « a priori » choisi. Or, il s’avère que, dans la majorité des cas, ce le choix de la probabilité a priori est arbitraire et qu’aucune valeur ne s’impose par elle-même. Ainsi, il devient de plus en plus fréquent qu’un essai ait simultanément le double objectif de mettre en évidence la supériorité du traitement étudié ou son équivalence. Ce qui montre qu’a priori une hypothèse particulière ne s’impose pas naturellement. C’est, par exemple, le cas dans l’essai VALIANT qui compare un inhibiteur de l’angiotensine 2 à un inhibiteur de l’enzyme de conversion (3).

4 Références

1. Browner WS, Newman TB. Are all significant P values created equal? The analogy between diagnostic tests and clinical research. JAMA 1987;257:2459-63.

2. Press SJ. Bayesian statistics: principles, models and applications. New-York: John Wiley & Sons; 1989.

3. Pfeffer MA, McMurray J, Leizorovicz A, Maggioni AP, Rouleau JL, Van De Werf F, et al. Valsartan in acute myocardial infarction trial (VALIANT): rationale and design. Am Heart J 2000;140(5):727-50.

Interprétation des essais cliniques pour la pratique médicale

www.spc.univ-lyon1.fr/polycop

Michel Cucherat

Faculté de Médecine Lyon - Laennec

Mis à jour : aout 2009