Hétérogénéité

Accueil > Sommaire > Hétérogénéité

1 Définition

L'hétérogénéité se définit par le rejet de l'hypothèse d'homogénéité des effets traitement. Le test de cette hypothèse est appelé test d'hétérogénéité ou test d'homogénéité, ce qui induit quelques confusions. Quel que soit son nom, l'hypothèse testée est la même et l'obtention d'un test significatif témoigne d'une hétérogénéité : l'effet d'un essai au moins ne peut pas être considéré comme étant identique à celui des autres essais. L'hypothèse du modèle fixe ne tient pas et la combinaison de tous ces essais devient litigieuse. En effet, la méta-analyse cherche à estimer une valeur qui, par hypothèse, est considérée comme commune à tous les essais.

Le test d'hétérogénéité possède une faible puissance avec le nombre d'essais habituellement rencontré dans les méta-analyses (en général inférieur à une trentaine). A contrario, avec un grand nombre d'essais, une faible hétérogénéité sans pertinence clinique est détectable.

Une hétérogénéité peut être le témoin d'une interaction entre une covariable et l'effet du traitement. Elle peut aussi provenir d'une forte variabilité aléatoire de l’effet sans qu'il soit possible de rattacher ces fluctuations à un ou des facteurs bien précis. L'effet est alors inconstant d'un essai à l’autre et pose la question du bien-fondé du regroupement de ces essais.

2 Statut de l’hétérogénéité

L'hétérogénéité peut être considérée comme une nuisance que l’on cherchera à éliminer en prenant une méthode adaptée (méthode à effet aléatoire, méthode de Peto). Ces techniques prennent en compte l'hétérogénéité sans chercher à l'expliquer.

A l'opposé, l’hétérogénéité peut être considérée comme informative, témoignant de changement dans l'effet du traitement en fonction des circonstances de sa mesure (profil des patients ou utilisation du traitement).

Statut de l'hétérogénéité	Approche
Nuisance	Prise en compte de l'hétérogénéité (sans l'expliquer) avec un modèle aléatoire
Information	Explication de l'hétérogénéité en fonction de covariables

3 Que faire devant une hétérogénéité

3.1 Recherche des essais induisant l’hétérogénéité

La première chose à faire devant une hétérogénéité est de rechercher le ou les essais qui l'induisent, en s'aidant d'un graphique. Pour confirmer les indications apportées par l'analyse graphique, l'hétérogénéité est recalculée, après suppression des essais suspects, pour s'assurer de sa disparition effective. Après avoir identifié les essais qui induisent l'hétérogénéité, il convient de chercher s'ils diffèrent des autres par l'une de leurs caractéristiques (populations, intervention, qualité méthodologique). Ensuite, si un facteur d'hétérogénéité est suspecté, non seulement le ou les essais induisant l'hétérogénéité devront être exclus de la méta-analyse, mais aussi tous les essais dans lesquels ce facteur est présent .

3.2 Recherche d'interaction

Une approche complémentaire consiste à rechercher systématiquement s'il existe une interaction avec une ou plusieurs covariables. Cette recherche d'interaction a pour but de montrer que la taille de l'effet varie en fonction des valeurs prises par une ou plusieurs covariables. Cette démonstration peut être obtenue par plusieurs moyens:

- les analyses en sous-groupes,

- la modélisation de l'effet sur les données résumées par des techniques uni- ou multi-variées,

- l'utilisation de modèles uni- ou multi-variés sur les données individuelles (ces techniques sont abordées dans le chapitre consacré aux m éta-analyses sur données individuelles, chapitre 28).

L'existence d'une hétérogénéité n'est pas une condition nécessaire à la recherche des interactions. Celle-ci peut être effectuée de manière systématique, lorsqu'elle correspond, par exemple, à l'un des objectifs de la méta-analyse. Dans ce cas les modalités de la recherche des interactions et les facteurs étudiés sont prévus d'emblée dans le protocole.

3.3 Modèle aléatoire

Si l'hétérogénéité observée ne s'explique pas par une interaction, il est possible de recourir à un modèle aléatoire. Ce modèle prend en compte une certaine variabilité aléatoire de l'effet traitement d'un essai à l'autre.

L'estimation obtenue tiendra compte de cette variabilité, l'intervalle de confiance de l’effet combiné sera plus large qu' avec le modèle fixe, et la variance du vrai effet traitement sera estimée (τ2). Les intervalles de confiance sont plus larges car, en plus des fluctuations aléatoires, ils prennent en compte la variabilité du vrai effet traitement.

L'utilisation d'un modèle aléatoire s'accompagne d'un risque de méconnaître l'existence d'une interaction et d'arriver à une conclusion réductrice qui perd une partie de l'information apportée par les essais.

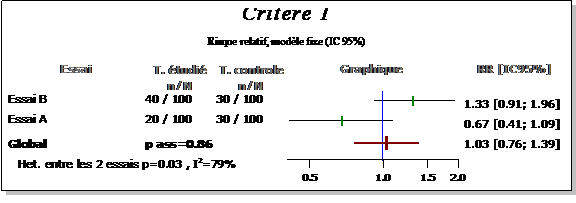
4 Analyses en sous-groupes

Les analyses en sous-groupes effectuent une recherche de l'interaction de façon univariée, en comparant les résultats obtenus entre deux ou un petit nombre de sous-groupes d'essais. Une interaction est détectée si les résultats des sous-groupes se révèlent statistiquement différents les uns des autres par l'application du test d'hétérogénéité entre les strates. Les sous-groupes sont créés en fonction de la covariable étudiée.

4.1 Hétérogénéité entre les sous-groupes

Une interaction entre l'effet du traitement et le facteur définissant les sous-groupes peut être recherchée par une analyse de l'hétérogénéité entre les sous-groupes. Cette analyse consiste en la réalisation de méta-analyses dans chacun des sous-groupes. L’hétérogénéité au sein de chaque sous-groupe est recherchée ainsi que l'hétérogénéité entre les résultats des sous-groupes. Une interaction se manifestera par des essais homogènes au sein de chaque sous-groupe, mais conduisant à une hétérogénéité entre les sous-groupes. L'effet du traitement est alors significativement différent d'un sous-groupe à l'autre (voir par exemple le cas du délai depuis les symptômes dans la figure 24.3)

Le test d'hétérogénéité des résultats dans chaque sous-groupe utilise la classique statistique Q:

4.2 Constitution des sous-groupes

Les sous-groupes pourront être définis de diverses façons :

1. par le type de traitement. Par exemple, dans la méta-analyse des hypocholestérolémiants il est possible de regrouper les essais en fonction des classes pharmacologiques (fibrates, inhibiteur de l'HMGCoA réductase, résines); en fonction de la molécule (simvastatine, lovastatine, pravastatine); en fonction de la nature de l'intervention (régime, médicaments, chirurgie). Des sous-groupes en fonction de la dose sont aussi envisageables ou en fonction du moment du traitement (par exemple avec les traitements fibrinolytiques dans l'infarctus du myocarde en fonction du délai d'administration par rapport au début des symptômes),

2. par le type de mesure du critère de jugement, lorsque plusieurs moyens existent pour mesurer le même critère de jugement. Par exemple, dans les essais de prévention du risque thrombo-embolique par les héparines, différents moyens diagnostiques sont utilisables pour rechercher les phlébites (clinique uniquement, phlébographie, Doppler, fibrinogène marqué),

3. par des caractéristiques propres aux patients. Par exemple, en fonction de la tranche d'âge, du sexe, en fonction du pronostic ou du risque de base,

4. 4. par les conditions de réalisation des essais : essais hospitaliers versus ambulatoires, en fonction de la région ou du pays de réalisation, etc...

5. par le type d'essais : essais en double aveugle, en simple aveugle.

Dans le premier cas, l'opération revient à comparer différents traitements par des comparaisons indirectes. Par contre, dans les autres cas, le but est de rechercher une modification de la taille de l'effet en fonction de facteurs divers, correspondant soit à des caractéristiques des patients, soit à des caractéristiques des essais. Il s'agit alors d'une véritable recherche d'interaction.

La définition des sous-groupes est fixée a priori dans le protocole, sauf dans le cas où le problème se pose après mise en évidence d'une hétérogénéité. Suivant les cas, les sous-groupes peuvent être constitués de deux façons :

1. Les essais sont répartis entre les différents sous-groupes car au sein d'un essai tous les patients sont identiques vis à vis de la caractéristique définissant les sous-groupes.

2. Chaque essai regroupe des patients qui correspondent aux différents sous-groupes. Ces patients doivent donc être répartis entre les différents sous-groupes. Cette situation exige que les données correspondant à chaque type de patients soient rapportées séparément dans le compte rendu de l'essai, c'est à dire que la même analyse en sous-groupe ait été réalisée dans l'essai. Si cette condition n'est pas remplie, seules les données individuelles permettront de recréer les sous-groupes.

4.3 Risque des analyses en sous-groupes

En méta-analyse, les analyses en sous-groupes (aussi appelées stratifiées) font courir, comme dans un essai clinique, le risque de l'inflation non contrôlée de l'erreur de première espèce. La multiplication des tests statistiques (un par sous-groupe) augmente la probabilité d'obtenir un test significatif uniquement par hasard. Un résultat de sous-groupe significatif devient suspect car il est impossible de savoir si ce test révèle une interaction réelle ou s'il s'agit simplement d'un artefact lié à la répétition des tests. Par exemple, dans l'essai ISIS-2, l'aspirine administrée à la phase aiguë de l'infarctus du myocarde produit une réduction significative très importante de la mortalité à 1 mois. Mais, lors de l’analyse en sous-groupe en fonction des signes astrologiques, l'aspirine apparaît inefficace pour les sujets du signe de la vierge ou des gémeaux et plus efficace que la moyenne pour le signe du capricorne. Dans les paradigmes scientifiques actuels, aucune théorie ne permet de penser que ces différences sont réelles!

En effet, il est toujours possible d'obtenir un résultat significatif en multipliant les sous-groupes. Un résultat significatif obtenu dans ces conditions n'a aucune valeur. La réalisation d’analyse en sous-groupes à partir de données issues de plusieurs essais dans une méta-analyse ne résoud pas ce problème (qui est uniquement lié à la répétition des tests).

4.4 Génération des hypothèses des sous-groupes

Pour minimiser le risque de résultats significatifs par hasard dans les analyses en sous-groupes, il convient de définir a priori un petit nombre de sous-groupes. Ces analyses s’apparenteront alors à la démarche hypothético-déductive.

Les sous-groupes définis a priori sont retenus de deux manières différentes.

1. certaines interactions peuvent être recherchées systématiquement avec, par exemple, l' âge, le sexe, la dose, la durée. Ces interactions sont suspectées de façon systématique ou à partir d'un modèle physiopathologique, pharmacologique ou thérapeutique.

2. Les interactions peuvent être suspectées à partir de résultats obtenus dans un des essais du domaine. L'hypothèse est générée par les données et il convient d'éviter tous risques de tautologie dans sa confirmation.

Dans cette dernière situation, la méta-analyse permet de confronter cette hypothèse à d'autres données externes à son processus de génération. Ainsi, il est possible de vérifier si un résultat initialement observé dans un essai se retrouve dans d'autres essais. Dans l'affirmative, les chances que ce résultat soit uniquement le fait du hasard s'amenuisent. A ce niveau, il est possible de discuter l'attitude qui consiste à exclure ou à maintenir l'essai (ou les essais) à l'origine de l'hypothèse dans la méta-analyse. En effet, si le poids de celui-ci est prépondérant dans la méta-analyse (car il comporte à lui tout seul autant de sujets que les autres réunis) le résultat de la méta-analyse ne dépendra presque exclusivement que du résultat de cet essai, conduisant a une confirmation tautologique de l'hypothèse. Une analyse de sensibilité confrontant les résultats obtenus avec et sans les essais à l'origine de l'hypothèse semble être la meilleure solution pour éprouver ce problème potentiel.

A contrario, la pratique de la méta-analyse a fourni des exemples du caractère fallacieux des analyses en sous-groupes dans les essais. Des relations statistiques apparemment fortes, quoique fortuites, entre les variables de base des patients et le résultat observé dans un essai ont été infirmées par la méta-analyse. C'est le cas de la relation entre la topographie de l'infarctus et l'effet des béta-bloquants dans le post-infarctus.

4.5 Apport de la méta-analyse par rapport aux analyses en sous-groupes dans les essais

La division de l'échantillon de patients en deux ou plusieurs sous-groupes entraîne une baisse de puissance des comparaisons réalisées dans chaque groupe et du test interaction. La méta-analyse apporte plus de patients et augmente la puissance par rapport à un seul essai.

Dans un essai isolé, le nombre de sujets inclus a été calculé pour assurer une puissance suffisante à la comparaison principale. Par rapport à cette comparaison, une recherche d'interaction nécessite plus de patients. Un seul essai est donc en général insuffisant pour garantir une puissance suffisante à une analyse en sous-groupes. La méta-analyse permettra de renforcer les effectifs et d'augmenter la puissance des comparaisons en sous-groupes.

Cependant, même dans le meilleur des cas, la mise en évidence d'une interaction reste du domaine de l'association statistique et ne permet pas de conclure à la relation causale entre le facteur étudié et la variation de la taille de l'effet. En effet, les différentes modalités du facteur étudié ne peuvent pas être contrôlées, ce qui empêche de se prémunir contre l'existence de facteur de confusion.

La méta-analyse classique ne permet que des analyses univariées en sous-groupes. L’ajustement de la recherche d'une interaction, sur d'éventuels facteurs de confusion est donc impossible sans le recours à des techniques multivariées.

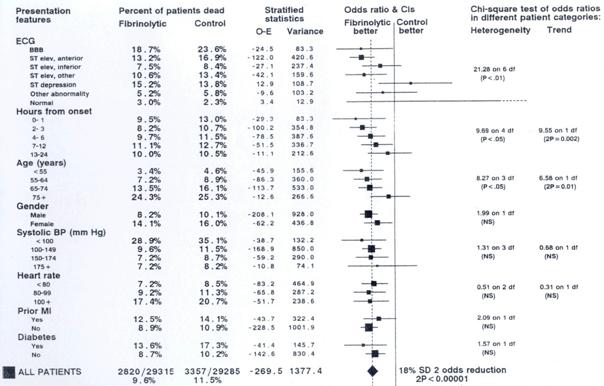
Exemple La méta-analyse du « Fibrinolytic Therapy Trialists' Collaborative Group » regroupe 9 essais de grande taille (> 1000 patients) de la fibrinolyse à la phase aiguë du myocarde. Plusieurs sous-groupes ont été étudiés, où une différence d'efficacité de la fibrinolyse était recherchée en fonction de caractéristiques des patients comme les signes ECG, le temps écoulé entre le début des symptômes et la fibrinolyse, l'âge, le sexe, l'existence d'un diabète ou d'antécédents d'infarctus du myocarde. La figure 24.3 représente les résultats de ces différents sous-groupes.

Fig. 24.3. — Exemple d'analyse en sous groupes

Interprétation des essais cliniques pour la pratique médicale

www.spc.univ-lyon1.fr/polycop

Michel Cucherat

Faculté de Médecine Lyon - Laennec

Mis à jour : aout 2009