Accueil > Sommaire > Mesures quantitatives
1 Les mesures quantitatives
Des variables quantitatives liées directement à un processus physiologique ou biologique peuvent être utilisées comme critère de jugement, comme la valeur d’un paramètre biologique, le résultat d’une épreuve fonctionnelle, etc. (Figure 9).
Tableau 8 – Exemple de critères de jugement basés sur des paramètres quantitatifs
|
Paramètre
biologique |
·
Charge virale (SIDA) ·
Taux de CD4 (SIDA) ·
Température (infections) |
|
Épreuve
fonctionnelle |
·
Périmètre de marche ( ·
Débit expiratoire forcé (asthme) |
|
Autres
types |
·
Échelle visuelle analogique (douleur) |
L’avantage des mesures quantitatives est d’être relativement sensible et de demander un petit nombre de patients afin de mettre en évidence les effets d’un traitement.
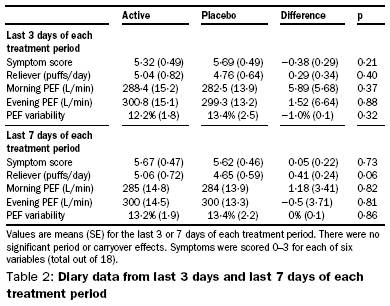
Figure 9 – Exemple de tableau rapportant les résultats obtenus au niveau de critères de jugement quantitatif.
1.1 Expression de l’effet
traitement
L’effet du traitement peut être mesuré de différentes façons (cf. chapitre Indices d’efficacités) :
· différence des valeurs moyennes mesurées en fin d’essai entre les deux groupes. Cette mesure n’est pas ajustée sur les valeurs initiales et sous-entend donc une comparabilité initiale forte des groupes (mêmes moyennes à l’inclusion).
· différence entre les deux groupes des changements moyens observés dans chaque groupe entre le début et la fin de l’essai.
La charge virale
La charge virale est couramment utilisée dans les essais de traitement de l’infection à VIH où elle est parfois considérée, seule ou en association avec le taux de CD4, comme un critère de substitution.
Les modifications de charge virale peuvent être exprimées de plusieurs façon.
a) Logarithme de la réduction obtenue en fin de l’essai. Pour chaque patient, le logarithme décimal de la valeur initiale de charge virale est soustrait au logarithme de la valeur mesurée en fin d’essais. La moyenne ou la médiane de ces résultats individuels sont ensuite calculées dans chaque groupe de l’essai. Le fait de travailler sur une échelle logarithme équivaut à calculer le rapport de la valeurs initiale sur la valeur finale de la charge virale. Par exemple, avec un dosage dont le seuil de détection est de 400 copies d’ARN/mL et un traitement qui rend indétectable la charge virale entraînera un changement de 3 log chez un patient dont la valeur initiale est de 400 000 copies/mL, et seulement un changement de 1 log chez un autre patient dont la valeur initiale est de 4 000 copies/mL. Cette mesure est donc sensible au seuil de détection du dosage utilisé. Chez un même patient, plus une méthode est sensible plus elle montrera un changement important. Il est donc important de connaître le dosage utilisé pour comparer les résultats de plusieurs essais.
b) Logarithme des pics de réduction. Avec cette méthode, la valeur de base est soustraite à la plus faible valeur de charge virale observée durant le suivi, quel que soit le moment de survenue de ce minimum. Cette différence est ensuite exprimée en terme logarithmique. Cette mesure est à proscrire car, avec un traitement sans effet, elle prend les fluctuations aléatoires vers le bas comme baisse engendrée.
c) Aire sous
L’interprétation d’une différence induite par un traitement sur une mesure quantitative et la détermination de sa signification clinique n’est pas toujours évidente.
1.2 Pertinence clinique
Comme avec les scores et les échelles, la pertinence clinique d’un effet traitement observé au niveau d’une mesure quantitative n’est pas toujours simple à établir. En plus, les mesures quantitatives font courir le risque de donner assez facilement des différences statistiquement significatives mais de faible ampleur et donc sans signification clinique. Les variables continues sont aussi plus souvent en rapport avec un critère intermédiaire qu’avec un critère clinique.
Par
exemple, quel est l’intérêt clinique d’un traitement
vasodilatateur augmentant de 20m en moyenne le périmètre de
marche de patients ayant une
Exemple
Dans l’incontinence urinaire féminine, un critère utilisé consiste à compter le nombre de fuites urinaires liées à un besoin impérieux sur une certaine période de temps, en général une semaine. Chez des femmes ayant en moyenne 20,7 fuites par semaine, un traitement apporte une réduction supplémentaire par rapport au placebo du nombre de fuites par semaine de 4,3 (le placebo étant associé avec une réduction de 8 par rapport aux valeurs initiales) (10). Ce qui ramène sous traitement la fréquence moyenne des fuites à 8,4 par semaine.
Cet effet hautement statistiquement signification (p<0.0001) est cependant très peu pertinent car ce qui gêne ces femmes, entre autres, c’est la nécessité de porter une protection. Avoir 8,4 fuites par semaine à la place de 20,7 jours ne solutionne pas leur problème car elles continuent à devoir porter des protections. Un critère plus pertinent consisterait à dénombrer les succès thérapeutiques : c'est-à-dire les femmes n’ayant plus de fuite sur une période de temps significative, ou éventuellement, dans les cas sévères, le nombre de protections utilisées par jour.
Cet exemple illustre donc le fait que les critères quantitatifs sont fréquemment sans pertinence clinique, non pas parce qu’ils correspondent à une entité nosologique sans intérêt, mais plutôt parce qu’ils peuvent facilement mettre en évidence des effets de petite taille et/ou parce que la gêne subie par les patients n’est pas proportionnelle à la valeur moyenne du critère.
Une solution est de binariser les mesures quantitatives (cf. infra) pour créer une variable binaire de succès-échec thérapeutique. Par exemple, chez les patients artériopathiques, un objectif thérapeutique pourrait être de rendre le périmètre de marche supérieur à 500m. Le bénéfice du traitement s’évaluera alors en termes de nombre de patients atteignant cet objectif.
1.3 Mesures
répétées
La mesure des critères continus est souvent répétée au cours du suivi d’un essai afin d’appréhender la dynamique de l’effet thérapeutique. L’analyse statistique présente cependant un certain nombre de difficulté (11, 12). La réalisation de plusieurs comparaison temps par temps se heurte au problèmes des comparaisons statistiques multiples. Des techniques statistiques pour mesures répétées sont disponibles mais nécessitent de faire des hypothèses fortes sur les données.
|
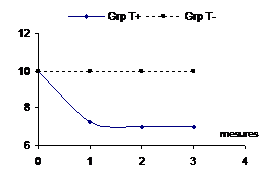
Effet permanent. Après avoir
s’être établi, l’effet du traitement se maintient
durant toute la période d’observation. |
|
|
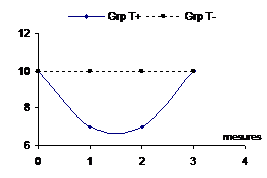
Effet temporaire. Il n’existe pas de
différence entre les deux groupes à la fin de l’essai,
mais un effet traitement a existé temporairement. |
|
|
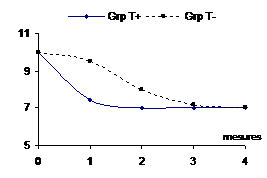
Il n’existe pas de différence
en fin d’essai, mais la réduction a été obtenue
plus rapidement dans un groupe que dans l’autre. |
|
Figure 10
– Différents cas de figures d’effet traitement possible avec
des mesures répétées d’un critère de jugement
quantitatif
Le moment de mesure de l’effet est donc un point important avec les critères de jugements continus.
1.3.1 Analyse statistique
Au niveau statistique, les mesures répétées (appelées aussi mesures longitudinales) donnent lieu à de nombreuses comparaisons statistiques conduisant à une inflation du risque alpha. Pour éviter cela, les données peuvent être comparées en bloc, avec, par exemple, une analyse de variance pour mesures répétées qui, si elle s’avère statistiquement significative, permet de dire qu’il existe un effet du traitement à au moins un moment de mesure. L’identification de ce ou ces moments pose ensuite toute une série de problèmes statistiques non entièrement résolus (non indépendance des mesures, répétition des tests statistiques, etc.).
Pour contourner ces difficultés, les mesures répétées peuvent être résumées par leur moyenne, par l’aire sous la courbe ou par un modèle d’évolution. La comparaison porte ensuite sur les paramètres résumés ce qui réduit à un le nombre de comparaison statistiques.
1.3.2 Exemple :
évaluation des antalgiques
L’évaluation
des antalgiques fait appel à des mesures quantitatives de
l’intensité de la douleur (13). L’outil le plus
fréquemment utilisé est l’échelle visuelle
analogique. On demande au sujet d’indiquer l’intensité de sa
douleur par une marque sur une ligne horizontal de
Dans un essai, ces mesures sont répétées au cours du temps afin d’étudier l’évolution chronologique de l’effet de l’antalgique. Afin d’exploiter l’ensemble de l’information apportée par la répétition des mesures, il est souhaitable d’intégrer ces multiples mesures afin de juger globalement de l’effet sur une période de temps donnée. Ces indices intégratifs sont calculés dans chaque groupe de l’essai et l’effet du traitement est déterminé par la différence existant entre le groupe expérimental et le groupe contrôle. Plusieurs types d’intégration sont possibles.
À chaque temps de mesure est calculé le PID (« pain intensity difference ») qui est la différence d’intensité de la douleur par rapport à la valeur basale. Ces valeurs permettent de déterminer le max PID qui est la valeur maximale de PID obtenue durant la période de temps ou Tmax PID qui est le temps d’obtention de l’effet antalgique maximum depuis la prise.
L’aire sous la courbe est appréciée par le SPID « sum of PID » qui est la somme de tous les PID.
D’autres indices comme le PAR (« pain relief ») sont basés, non plus sur l’intensité de la douleur mais sur son soulagement. Pour cela, l’échelle visuelle analogique utilisée porte à son extrémité gauche la mention « aucun soulagement » et son extrémité droite « soulagement complet ». Là aussi on peut établir un max PAR ou un Tmax PAR. Un score global, le TOTPAR (« Total of Pain relief »), est calculé en utilisant l’aire sous la courbe pour une période de temps définie. Le TOTPAR s’exprime aussi en pourcentage du TOTPAR maximum qui serait obtenue par un traitement qui donnerait un soulagement complet durant la période d’observation.
2
Binarisation
Une solution aux problèmes d’interprétation clinique des effets mesurés par des échelles, des scores ou des variables continues est de les transformer en une variable binaire en fonction d’une valeur seuil. Cette transformation exprime le résultat en termes de succès thérapeutiques. L’effet du traitement est alors mesuré, par exemple, par la proportion de patients ayant un score supérieur (ou inférieur) à la valeur seuil..
En général, la binarisation est construite de façon à séparer les patients sévèrement atteints de ceux qui le sont moins : score de dépression important, périmètre de marche très limité.
Une autre façon est de choisir un seuil qui correspond à une guérison ou à une quasi-guérison. Dans ce cas, la variable binaire évalue la proportion de patients guéris par le traitement. C’est par exemple le cas avec l’hypertension artérielle où il est possible de créer une variable binaire : normalisation de la pression artérielle (Cette variable ne correspond cependant pas à un critère clinique : une variable binaire ne correspond pas automatiquement à un critère clinique). La binarisation peut aussi être basée sur un seuil de changement de la variable continue : par exemple une amélioration de plus de 30% du périmètre de marche. Cette définition du succès thérapeutique peut manquer de pertinence clinique si l’on prend un seuil d’amélioration peu ambitieux. D’autres définitions sont possibles faisant intervenir la durée de l’amélioration (maintient au-dessus du seuil durant au moins x jours, etc…), ou un objectif fixé par le patient lui même.
2.1
Exemple de l’ACR20
L’American College of Rheumatology a défini un critère pour mesurer l’efficacité des traitements de fonds de la polyarthrite rhumatoïde (antirhumatismaux d’action lente), l’ACR20. Ce critère est défini d’une part par une amélioration d’au moins 20% à la fois du nombre d’articulations douloureuses et du nombre d’articulations tuméfiées, et d’autre part par une amélioration d’au moins 20% du score des critères suivants : évaluation globale par le malade, évaluation globale par le médecin, score à l’échelle HAQ (Health Assessment Questionnaries) ou sa version modifiée M-HAQ remplie par le malade, et soit l’amélioration de la vitesse de sédimentation, soit du taux de protéine C réactive. L’effet d’un traitement est évalué en comparant le pourcentage de patients satisfaisant ce critère.
Le taux de patient ACR 20% est actuellement largement utilisé mais sa signification clinique est controversée (14Ê, 15). Par exemple, une réduction de 20% peut simplement traduire que les articulations douloureuses ou tuméfiées est passé de 15 à 12, ou de 5 à 4.
D’autres critères, comme ACR 50 ou ACR 70 sont obtenus de la même façon qu’ACR 20 en exigeant des taux d’amélioration de 50% ou 70%. Comparé avec ces deux indices, l’ACR 20 conduit plus facilement à des différences statistiquement significatives entre traitement et placebo, mais sa pertinence clinique est discutée. Malgré cela, la plupart des essais sont actuellement réalisés avec la mesure de ce critère au bout de 6 mois.
Les constituants de l’ACR 20 sont en fait des mesures de l’activité inflammatoire réversible. Ces mesures sont utilisées comme critère intermédiaire à la place de l’évaluation des dégâts articulaires comme l’érosion radiographique, de la déformation articulaire ou de toute autre évolution au long terme.
De ce fait, des essais au long cours restent nécessaires pour mieux évaluer la progression de la PR sur des critères pertinents : déformations des articulations, handicap fonctionnel, nécessité d’intervention chirurgicale articulaire, manifestations extra articulaires, mortalité.
2.2
Problèmes divers posés par la binarisation
Bien que la binarisation permette de mieux appréhender la pertinence d’un effet, celle-ci n’est que rarement effectuée. De plus, lorsqu’elle est faite, il est rare que le même seuil soit utilisé d’un essai à l’autre. Il semble alors difficile de comparer les résultats des essais entre eux. En fait, il est possible de démontrer que sous certaines conditions, l’odds ratio calculé après binarisation est assez indépendant de la valeur du seuil et dépend surtout de la différence entre les deux distributions (c’est-à-dire entre les moyennes par rapport à leur variance). Ainsi, la comparaison d’études est possible même si des seuils différents ont été utilisés.
Les mêmes propriétés donnent le moyen de calculer un odds ratio même si aucune binarisation n’est disponible. Ainsi, il devient possible d’exprimer l’effet du traitement en termes d’odds ratio, comme si une binarisation avait été effectuée, et si l’on compare plusieurs essais, comme si le même seuil de binarisation avait été utilisé.
Bien entendu, ces calculs sont des extrapolations qui ne sont exactes que si les distributions des variables continues suivent une distribution particulière, la distribution logistique, qui est proche de la distribution normale. La méthode est relativement robuste à une déviation de la loi normale à conditions qu’elle reste symétrique.
Calcul d’un odds ratio à partir d’une différence de moyenne
La première des figures ci-dessous représente l’évolution de la fréquence du critère binaire dans les 2 groupes en fonction du seuil de binarisation utilisé (loi normale). La seconde figure représente l’évolution de l’odds ratio (RC) en fonction de ce seuil de binarisation.


Lorsque l’on représente l’odds ratio en fonction de
la fréquence du critère binaire dans le groupe contrôle (r0),
il apparaît que l’odds ratio reste presque inchangé pour une
large étendue de risque de base (de 15 à 85%).
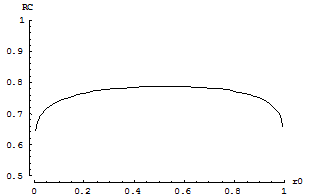
Ainsi, lorsque la distribution de la variable continue est proche
d’une distribution normale, l’odds ratio obtenu après
binarisation est quasiment indépendant de la valeur du seuil choisie
pour la binarisation, tant que cette binarisation ne conduit pas à une
fréquence du critère proche de 0% ou de 100%. De ce fait, un odds
ratio extrapolé à partir de la différence des moyennes
représente correctement celui qui aurait été obtenu lors
d’une binarisation.
L’extrapolation d’un odds ratio à partir d’une différence de moyenne se calcule de la façon suivante.
On fait l’hypothèse que la distribution de la variable continue est normale (au pire symétrique) et de même variance dans les deux groupes. L’odds ratio est alors obtenu par :
![]()
où ![]() et
et ![]() représente les deux moyennes et
représente les deux moyennes et
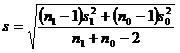 .
.
![]() et
et ![]() désignent les variances et n1 et
n0 les effectifs des deux groupes.
désignent les variances et n1 et
n0 les effectifs des deux groupes.
La variance du logarithme de l’odds ratio est :
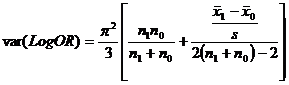
3 Bibliographie
1. Gerin P, Dazord A, Boissel JP, Hanauer MT, Moleur P, Chauvin F. L'évaluation de la qualité de vie dans les essais thérapeutiques. Thérapie 1989;44:355-64.
2. Schraub S, Mercier M, Arveux P. Mesure de la qualité de vie en cancérologie. Presse Med 2000;29:310-18.
3. Fleming TR, DeMets DL. Surrogate endpoints in clinical trials: are we being misled? Ann Intern Med 1996;125:605-613.
4. Greenhalgh T. How to read a paper: papers that report drug trials. BMJ 1997;315:480-483.
5. Advanced colorectal cancer meta-analysis project. Modulation of fluorouracil by leucovorin in patients with advanced colorectal cancer: evidence in terms of response rate. J Clin Oncol 1992;10:896-903.
6. Riggs BL, Hodgson SF, O'Fallon WM, Chao EY, Wahner HW, Muhs JM. Effect of floride treatment on teh fracture rate in postmenopausal women with osteoporosis. NEJM 1990;322:802-809.
7. The Long Term Intervention with Pravastatin in Ischaemic Disease (LIPID) Study Group. Prevention of cardiovascular events and death with pravastatin in patients with coronary heart disease and a broad range of initial cholesterol levels. NEJM 1998;339:1349-57.
8. Serruys PW, van Hout B, Bonnier H, Legrand V, Garcia E, Macaya C, et al. Randomised comparison of implantation of heparin-coated stents with balloon angioplasty in selected patients with coronary artery disease (Benestent II). Lancet 1998;352(9129):673-81.
9. Cohn JNG, S.O. A dose-dependant increase in mortality with vesnarinone among patient with severe heart failure. Vesnarinone Trial Investigators. NEJM 1998;339:1810-6.
10. Khullar V, Hill S, Laval KU, Schiotz HA, Jonas U, Versi E. Treatment of urge-predominant mixed urinary incontinence with tolterodine extended release: a randomized, placebo-controlled trial. Urology 2004;64(2):269-74; discussion 274-5.
11. Liu C, Li Wan Po A, Blumhardt LD. "Summary measure" statistics for assessing the outcome of treatment trials in relapsing-remitting multiple sclerosis. J Neurol Neurosurg Psychiatry 1998;64:726-729.
12. Senn S, Stevens L, Chaturvedi N. Repeated measures in clinical trials: simple strategies for analysis using summary measures. Stat Med 2000;19:861-877.
13. Dubray C. Etude clinique des médicaments antalgiques. Thérapie 1999;54:135-145.
14. Pincus T, Stein CM. ACR20: clinical or statistical significance? Arthritis Rheum 1999;42:1572-1576.
15. van Gestel A, van Riel L. Improvement criteria - clinical and statistical significance: comment on the article by Pincus and Stein. Arthritis Rheum 2000;43:1658-1659.
16. Bolton S. Independence and statistical inference in clinical trial designs: a tutorial review. J Clin Pharmacol 1998;38(5):408-12.
17. Altman DG, Bland JM. Statistics notes. Units of analysis. BMJ 1997;314(7098):1874.
18. Rodgers A, MacMahon S. Systematic underestimation of treatment effects as a result of diagnostic test inaccuracy: implications for the interpretation and design of thromboprophylaxis trials. Thrombosis and Haemostasis 1995;73:167-71.
Interprétation
des essais cliniques pour la pratique médicale
www.spc.univ-lyon1.fr/polycop
Faculté de Médecine Lyon - Laennec
Mis à jour : aout 2009