1 La différence des risques

1.1 Définition et calcul

La différence des risques (« risk difference »), appelée aussi différence absolue ou bénéfice absolu, est égale à la différence entre le risque sous traitement (r₁) et le risque sans traitement (r₀). Elle se calcule par :

Le calcul de la différence des risques à partir des données de l’exemple donne :

DR = 0,08 - 0,15 = 0,07 soit –7%.

La différence des risques donne la taille de l’effet non ajustée sur la valeur initiale.

Il est possible de rapporter la différence des risque sous forme de réduction absolue des risques RAR («absolute reduction in risk») qui est égale à :

Figure 5 – Exemple d’essai quantifiant les effets à la fois avec un risque relatif et la réduction absolue des risques (1-DR)

1.1 Interprétation

En l’absence d’effet du traitement, la différence est nulle. Un effet bénéfique se traduit par une différence des risques négative et un effet délétère par une valeur positive. Plus la valeur absolue de la différence de risque est importante plus l’effet est grand. Une différence des risques de -7% signifie que le traitement évite la survenue de 7 événements pour 100 patients traités.

Parfois, la différence des risques est calculée comme étant la différence entre le risque sans traitement et celui avec traitement : r₀-r₁ (avec les données de l’exemple cela donne 0,015-0,08 = 0,07). Dans ce cas, la signification de la différence des risques est inversée : valeur positive pour un effet bénéfique, valeur négative pour une effet délétère. La première définition présente l’avantage de localiser sur un graphique les valeurs correspondantes à un effet bénéfique à gauche de la valeur témoignant l’absence d’effet, de la même façon qu’avec le risque relatif ou l’odds ratio.

Calcul de l’intervalle de confiance

Les bornes de l’intervalle de confiance à 95% de la différence des risques s’obtiennent par :

où var(DR) désigne la variance de la différence des risques dont une approximation est :

2 Le NNT

Cet indice nommé par l’abréviation NNT pour Nombre de sujet Nécessaire de Traiter (ou en anglais « Number Needed to Treat ») correspond au nombre moyen de sujets qu’il est nécessaire de traiter pour éviter 1 événement. Il est égal à l’inverse de la différence des risques :

Dans notre exemple, le NNT est égal à NNT = 1/-0,07 = -14. Le signe moins témoigne d’un effet bénéfique et l’interprétation en fonction du signe est identique à celle de la différence des risques.

Attention, pour le calcul du NNT, la différence des risques ne doit pas être exprimée en pourcentage. En effet, 1/7=0,14 n’est pas la bonne valeur du NNT (rappel 7%=0,07).

Un NNT de 14 signifie qu’il faut traiter en moyenne 14 patients pour éviter un événement. En effet, sans traitement le nombre d’événements attendu chez 14 sujets est de 14×0,15=2,1 tandis que sous traitement ce nombre est de 14×0,08=1,1, ce qui correspond bien à un patient de moins. En moyenne, tous les NNT patients traités, un événement est évité.

Exemple

“Treatment with atorvastatin 10 mg daily for 4 years in 1000 such patients would prevent 37 first major cardiovascular events … . One major first cardiovascular event would be avoided for every 27 patients treated for 4 years. We have expressed these measures of absolute benefit at our median duration of follow-up of 4 years” D’après ref. ¹.

2.1 Différence des risques, NNT et durée de suivi

Le NNT et la différence des risques, dépendent de la durée de suivi ². Celle-ci doit donc toujours être précisée quand on rapporte ces indices. Le tableau 4 présente l’évolution au cours du temps des risques absolus avec et sans traitement, de la différence des risques et du NNT dans une situation où le risque annuel est de 5% et le risque relatif constant et égal à 0,80. Plus la durée de suivi est longue, plus le risque sans traitement est élevé. La différence des risques augmente aussi avec la durée de suivi alors que le NNT diminue. Cette relation entre NNT et différence de risque et durée de suivi doit être prise en compte lorsque l’on compare différents traitements.

Tableau 4 – Évolution en fonction de la durée de suivi de la différence des risques et du NNT

2.2 NNT et différence de risque

Différence des risques et NNT véhiculent la même information et quantifient le nombre d’événements évités par nombres de patients traités. En effet, cette information peut être exprimée :

· soit en nombre d’événements évités pour 100 (ou 1000) patients traités,

· soit en nombre de patients à traiter pour éviter 1 événement.

Par exemple, une différence des risques de 3/100 signifie que le traitement de 100 sujets durant la période de suivi de l’essai a permis d'éviter la survenue de 3 événements. La même situation correspond à un NNT de 33 signifiant qu’il faut traiter 33 patients durant la période de suivi de l’essai pour éviter 1 événement.

2.3 Interprétation

Depuis son introduction par Sackett ³, cet indice obtient un grand succès, car il semble très « parlant » pour les praticiens. Par exemple, à partir du nombre de patients souffrant de la maladie étudiée présent dans la clientèle d'un médecin, il estime le nombre d'événements que le traitement pourrait éviter. Il mesure en quelque sorte « l'énergie » moyenne qu'il faut dépenser pour obtenir un succès thérapeutique.

Son expression en termes d’un événement évité pour NNT patients traités a cependant tendance à faire croire qu'il existe réellement un individu qui ne présentera pas l'événement avec le traitement alors qu'il l'aurait présenté sans traitement. Il y a individualisation du bénéfice, mais cette interprétation est fausse. Cet indice est issu d'un développement valable en moyenne, et l'interprétation la plus probable est que tous les patients bénéficient un peu du traitement (il y a réduction de leur probabilité de faire un événement) et que cette réduction se traduit en moyenne par une différence de 1 du nombre moyen d'événements attendus sans et avec traitement dans un groupe de NNT patients.

Lorsque l’on dit qu’il faut traiter, par exemple, 30 patients pour éviter un événement, la tentation est forte de traduire cela en : un patient bénéficie du traitement tous les 30 patients traités. Par extension, sur 30 patients traités, 29 n’en bénéficient pas. Cette interprétation est abusive en personnalisant trop le bénéfice. Par exemple, il se peut que tous les patients bénéficient un peu du traitement en ayant par exemple leur espérance de vie augmentée de quelques mois. Donc aucun patient ne bénéficie plus que les autres.

Exemple de sur-interprétation du NNT

"There's a lot of expensive technology. Some of it provides benefit for only a tiny fraction of patients and at great cost" to everybody else, Sox says. With breast cancer, for example, 800 women must be screened for 13 years to prevent a single death. Yet, women aren't going to eschew mammography because of the cost to society of the test. (http://www.healthscout.com/template.asp?page=newsdetail&ap=1&id=507477 visité le 24/04/05).

Pour un même domaine thérapeutique, le NNT (comme le bénéfice absolu) varie plus d’un essai à l’autre que le bénéfice relatif (mesuré par un risque relatif ou odds ratio) car le risque de base varie souvent d’un essai à l’autre. Ce point a d’ailleurs été objectivé empiriquement ⁴. Le tableau 5 compare les risques relatifs et les NNT obtenus dans 4 essais comparant une statine au placebo dans la prévention des maladies cardiovasculaires ⁵.

Pour cette raison, les NNT ne doivent pas être utilisés pour comparer deux essais, encore moins pour comparer deux traitements concurrents pour une même pathologie. Des différences de NNT pouvant témoigner aussi bien d’une différence d’efficacité des traitements que de différences de risques de bases des patients entre les essais. La comparaison des NNT de deux traitements nécessite de se baser sur des NNT correspondant à un même risque base ⁶. Cette standardisation est obtenue en calculant les NNT à partir des risques relatifs et d’un risque de base de référence.

Tableau 5. Comparaison des risques relatifs et des NNT concernant les événements coronariens observés dans 4 essais de prévention du risque cardiovasculaire par les statines.

	Risque relatif	NNT (DR)	Risque de base
WOSCOPS	0,70	44 (23‰)	7,5%
CARE	0,77	33 (30‰)	13,1%
LIPID	0,77	28 (35‰)	15,9%
4S	0,70	15 (67‰)	22,6%

Pour un risque de base fixé R_c, le NNT s’obtient à partir du risque relatif RR par la formule :

Par exemple, avec un traitement caractérisé par un risque relatif de 0,8, le NNT correspondant à un risque de base de 10% est égal à 1/(0,1*0,2)=50. En effet, sous traitement, le risque est 0,1*0,8=8% ce qui donne une différence des risques de 10%-8%=2% soit un NNT=1/0,02=50.

La comparaison des bénéfices absolus de différents traitements doit s’effectuer à risque de base identique.

Le tableau 6 illustre les pièges tendus par la comparaison directe des NNT de deux traitements évalués dans des essais différents. À partir des NNT obtenus par les essais, on serait amené à conclure que le traitement A apporte un plus grand bénéfice absolu que le traitement B. Cependant, cette conclusion est erronée car le risque de base de l’essai évaluant le traitement B est plus petit que celui de l’essai du traitement A. En utilisant un NNT standardisé, par exemple pour un risque de base de 10% (qui se situe au milieu des risques des essais), il apparaît que le traitement B apporte un plus fort bénéfice absolu que le traitement A.

Tableau 6. Comparaison des NNT de deux traitements évalués dans des essais différents.

	NNT observé dans l’essai	Risque relatif	Risque de base	NNT standardisé pour un Rc=10%
Essai A (traitement A)	35	0,81	0,15	52
Essai B (traitement B)	53	0,69	0,06	32

2.4 NNH

La notion de NNT peut être étendue aux événements délétères. Il s’agit alors du « Number needed to harm (NNH) » qui quantifie le nombre de patients qu’il faut exposer au traitement pour observer, en moyenne, un effet indésirable du traitement (cf. chapitre Rapport bénéfice risque).

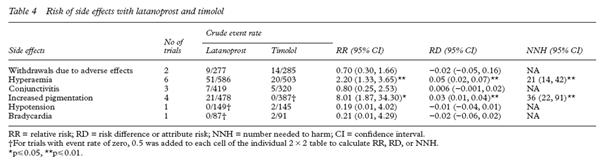
Figure 6 – Exemple de quantification des événements indésirables faisant appel au NNH. D’après ref. ⁷.

2.5 Calcul de l’intervalle de confiance d’un NNT

Il n’existe pas de méthode de calcul satisfaisante de l’intervalle de confiance du NNT

Un autre problème posé par le NNT est que le calcul de son intervalle de confiance n’est pas direct.

La première idée qui vient à l’esprit est de prendre comme borne de l’intervalle de confiance du NNT l’inverse des bornes de l’intervalle de confiance de la différence des risques. Ainsi à partir d’une différence des risques de 0,07 avec un IC95% = [0,02 ;0,12], on obtient un NNT de 14,3 avec comme borne de son intervalle de confiance 1/0,02=50 et 1/0,12=8,3 soit comme IC95% [8,3 ;50].

Un problème survient avec cette méthode lorsque les bornes de l’intervalle de confiance de la différence des risques sont de part et d’autre de zéro. En effet, avec une différence de risque de 0,01 dont l’IC95% est [–0,04 ;0,06] le calcul précédent donne comme borne 1/-0,04=-25 et 1/0,06=16,6 soit un IC95%=[-25 ;16,6] pour un NNT de 1/0,01=100. L’estimation ponctuelle (100) est située en dehors de l’intervalle de confiance. Ce phénomène provient de la nature hyperbolique de la transformation 1/x. Une méthode de calcul non entièrement satisfaisante a été proposée par Doug Altman ⁸, et une autre par R Bender ⁹.

3 Bibliographie

1. Randomised trial of efficacy and safety of inhaled zanamivir in treatment of influenza A and B virus infections. The MIST (Management of Influenza in the Southern Hemisphere Trialists) Study Group. Lancet 1998;352(9144):1877-81.

2. Lubsen J, Hoes A, Grobbee D. Implications of trial results: the potentially misleading notions of number needed to treat and average duration of life gained. Lancet 2000;356:1757-59.

3. Sackett DL. On some clinically useful measures of the effects of treatment. Evidence Based Medecine 1996;1:37-38.

4. Schmid CH, Lau J, McIntosh MW, Cappelleri JC. An empirical study of the effect of the control rate as a predictor of treatment efficacy in meta-analysis of clinical trials. Stat Med 1998;17:1923-42.

5. Cucherat M, Lièvre M, Gueyffier F. Clinical benefits of cholesterol lowering treatments. Meta-analysis of randomized therapeutic trials. Presse Med 2000;29:965-76.

6. McQuay HJ, Moore AR. Using numerical results from systematic review in clinical practice. Anns of Internal Medicine 1997;126:712-20.

7. Zhang WY, Po AL, Dua HS, Azuara-Blanco A. Meta-analysis of randomised controlled trials comparing latanoprost with timolol in the treatment of patients with open angle glaucoma or ocular hypertension. Br J Ophthalmol 2001;85(8):983-90.

8. Altman DG. Confidence intervals for the number needed to treat. BMJ 1998;317(7168):1309-12.

9. Bender R, Lange S. Adjusting for multiple testing - when and how? J Clin Epidemiol 2001;54(4):343-9.

Interprétation des essais cliniques pour la pratique médicale

www.spc.univ-lyon1.fr/polycop

Michel Cucherat

Faculté de Médecine Lyon - Laennec

Mis à jour : aout 2009