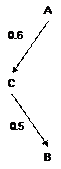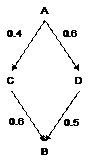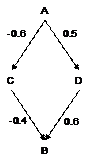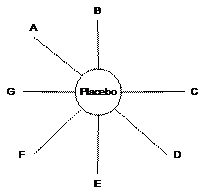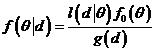Les différentes techniques de
comparaison indirecte
Accueil > Sommaire > Comparaison indirecte
De manière générale, toutes techniques produisant une estimation de l’effet (risque relatif, odds ratio, différence de risque, hazard ratio, différence de moyenne) de A par rapport à B à partir des estimations de l’effet de A versus contrôle et de B versus contrôle permet de réaliser des comparaisons indirectes.
Trois grands types de méthodes sont décrits dans ce chapitre :
· les méthodes non-valides, inappropriées,
· les méthodes de comparaisons indirectes ajustées, comparant les traitements 2 à 2,
· les méthodes modélisant simultanément tous les traitements concurrents dans la situation pathologique envisagée.
1 Les techniques inappropriées
Deux méthodes régulièrement utilisées dans la littérature sont impropres à réaliser des comparaisons indirectes valides. Aucune terminologie fixée n’est disponible pour désigner ces méthodes. Nous proposons de les identifier par la description de leur principe : comparaisons naïves des estimations ponctuelles ou des bras actifs issus d’essais contrôlés distincts.
1.1 Comparaison naïve des estimations ponctuelles
L’approche consistant à comparer l’estimation ponctuelle de l’efficacité de A vs placebo à celle de B versus placebo est inappropriée. Elle vient spontanément à l’esprit mais malheureusement elle présente de très nombreuses limites. Pour alléger l’exposer nous nous référons à des comparaisons versus placebo. Néanmoins, tout ce qui est dit est valable quelque soit le comparateur utilisé : placebo, soins standards, traitement actif
Il s’agit, par exemple, de comparer le risque relatif obtenu sur la mortalité lors de l’évaluation de A versus placebo à celui obtenu lors de l’évaluation de B versus placebo. Tout autre indice d’efficacité (réduction relative de risque, odds ratio, réduction relative des odds, différence de risque, nombre de sujets à traiter (NST), différences absolue ou relative de moyennes,…) peut être théoriquement employé à la place du risque relatif. Le traitement entraînant la plus grande réduction relative de risque sera qualifié plus efficace que l’autre.
Par exemple, les deux traitements A et B ont donné lieu à un essai de mortalité chacun dont les résultats sont représentés dans le Tableau 1.
Tableau 1 – Résultats des estimations ponctuelles de l’essai A vs placebo et de l’essai B vs placebo
|
|
Risque relatif |
|
Traitement A (versus placebo) |
0.76 |
|
Traitement B (versus placebo) |
0.87 |
Le traitement A entraîne une réduction relative de mortalité de 24%, plus importante que le traitement B (13%). A sera donc qualifié le plus efficace.
En dehors de toutes considérations sur la méthodologie des essais, sur les populations incluses et les traitements délivrés, la principale limite de cette approche est de ne pas tenir compte de la précision statistique des estimations. En fait, il se peut très bien que l’estimation la plus favorable soit aussi celle qui a l’intervalle de confiance le plus large, et donc une borne péjorative de l’intervalle de confiance compatible avec une faible efficacité. Dans ce cas, la conclusion prise à l’aide des estimations ponctuelles, privilégiera le traitement dont le bénéfice minimal garanti est le plus faible, au détriment de celui qui nous assure qu’il apporte un bénéfice supérieur, même dans le pire des cas d’erreur statistique sur l’estimation. Cette situation est illustrée dans le Tableau 2.
Tableau 2 – Résultats des estimations ponctuelles et intervalles de confiance de l’essai A vs placebo et de l’essai B vs placebo
|
|
Risque relatif IC 95% |
|
Traitement
A (versus placebo) |
0.76 [0.53;0.99] |
|
Traitement
B (versus placebo) |
0.86 [0.84;0.90] |
Avec le traitement B, une réduction de mortalité d’au moins 10% est garantie avec un degré de certitude de 95% tandis qu’avec A nous n’avons l’assurance que d’une réduction de 1% (avec un degré de certitude de 95%).
La prise en considération de la borne péjorative de l’intervalle de confiance montre que la comparaison des estimations ponctuelles est inappropriée. Elle ne permet pas d’obtenir une méthode satisfaisante de comparaison indirecte. Le raisonnement se focalise sur une seule possibilité bien particulière (la borne péjorative de l’intervalle de confiance) et néglige l’ensemble des autres possibilités offertes par l’intervalle de confiance. Les méthodes développées contournent ce problème.
De plus, la réalisation de ce type de comparaisons avec des différences de risques ou des NST est faussée par les éventuelles différences de risques de base entre les essais.
1.2 Comparaison naïve des bras actifs
Une autre approche inappropriée consiste à considérer les bras traitements actifs des essais sans tenir compte de la randomisation, c’est-à-dire de leur appariement au sein de l’essai.
A partir des deux essais A versus placebo et
B versus placebo, seules sont utilisées les données du bras A du
premier essai et celles du bras B du second essai. Les deux bras placebo sont
en quelque sorte mis de coté. L’effet de A vs B est alors
estimé en comparant les résultats du bras A à celui du
bras B. De ce fait, plus aucun contrôle des facteurs de confusion propres
à chaque étude n’est effectué. Il y a perte totale
du caractère contrôlé des deux essais. Le résultat
obtenu n’est plus à l’abri d’un biais de confusion. De
même, il y a perte totale du bénéfice de
Par exemple,
à partir des résultats présentés dans les Tableau 3
et Tableau 4,
cette approche comparerait 45/1567 à 36/1251 soit 2.87% à 2.88%.
Cette comparaison inciterait à conclure qu’il n’est pas
possible de considérer A comme plus efficace que B. Cette conclusion est
paradoxale puisque que l’examen des deux essais montre que A est efficace
par rapport au placebo tandis que B n’a pas montré son
efficacité.
Tableau 3 – Résultats de l’essai comparant A au placebo
|
|
Traitement A |
Placebo |
Risque
relatif |
|
Décès |
45/1567
(2.87%) |
103/1546
(6.66%) |
0.43 |
Tableau 4 – Résultats de l’essai comparant B au placebo
|
|
Traitement B |
Placebo |
Risque
relatif |
|
Décès |
36/1251
(2.88%) |
42/1298
(3.24%) |
0.89 |
En plus des arguments théoriques contre la validité de cette approche (cf. supra), le caractère biaisé de cette approche a été montré de manière empirique (1).
Cette approche, complètement invalide sur le plan méthodologique, est à l’origine des réticences actuelles contre les comparaisons indirectes. Ce fut la première méthode utilisée, mais le problème qu’elle pose n’est pas consubstantiel aux comparaisons indirectes. Les méthodes spécialement développées solutionnent cette difficulté comme il sera démontré dans la section 1.2.1.
L’étude
de cas de
1.3 Les comparaisons indirectes ajustées
L’estimation indirecte ajustée (« adjusted indirect comparison ») est la première méthode valide disponible pour faire des comparaisons indirectes.
1.4 Principe
Cette méthode de comparaison indirecte deux à deux fait la composition de l’estimation de l’effet de A versus placebo avec celle de B versus placebo. De ce fait, elle ne détruit pas la randomisation et conserve les propriétés méthodologiques de l’essai contrôlé randomisé.
Le calcul nécessaire est très simple. Considérons par exemple le cas où le critère de jugement d’intérêt est binaire et où l’effet est mesuré par un risque relatif.
Soit RRa le risque relatif issu de la comparaison du traitement A au placebo et RRb celui trouvé lors de la comparaison du traitement B au placebo. Le résultat de la comparaison indirecte A versus B est le risque relatif RRa/b, obtenu par
Le calcul de l’intervalle de confiance de ce risque relatif passe par le calcul de l’intervalle de confiance de son logarithme, en utilisant comme variance la somme des variances des logarithmes des deux risques relatifs
À partir de cette variance, l’intervalle de confiance du risque relatif RRa/b s’obtient de façon standard.
Un calcul similaire autorise l’extrapolation du bénéfice par rapport au placebo d’un nouveau traitement à partir du RR de ce traitement par rapport au traitement de référence et du RR du traitement de référence par rapport au placebo. Ce calcul est utile avec l’essai de non-infériorité
La démonstration de l’équation est très simple. Dans un essai de comparaison directe, les patients ont un risque d’événement sans traitement de r0. Dans le bras recevant A, le risque sous traitement ra devient
où RRa désigne comme précédemment l’effet de A par rapport à « pas de traitement » (mesuré dans une comparaison A versus placebo).
De manière identique, le risque sous traitement rb dans le bras du traitement B est
L’effet de A par rapport à B dans cet essai est mesuré par le risque relatif RRa/b qui est par définition
qui devient en utilisant les équations et
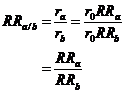
Ce qui justifie le calcul de la comparaison indirecte ajustée.
Dans ces calculs, le risque de base r0 disparait complètement. Cette extrapolation, basée sur les mesures des effets est donc totalement insensible au risque de base des essais de A et de B. La comparaison indirecte est donc valide même si les patients étudiés dans les essais de A et de B ne sont pas les mêmes. La condition de validité se trouve ailleurs, comme cela est détaillé dans la section qui suit.
1.5 Condition de validité : la stabilité des effets
Pour que cette approche donne un résultat qui a un sens médical, il faut qu’il y ait une certaine cohérence entre les deux risques relatifs RRa et RRb. C’est-à-dire que, dans les conditions (critères de gravité de la pathologie, caractéristiques des patients, traitements concomitants, etc.) où le traitement B a été évalué contre placebo, l’évaluation du traitement A aurait donné le même risque relatif que celui qui a été observé dans les essais de A versus placebo effectivement réalisé (la réciproque devant aussi être vérifiée).
En d’autres termes, cette condition implique que les essais versus placebo de A et B soient similaires en termes de covariables d’interaction avec les traitements, c’est-à-dire qu’il y ait stabilité des effets pour les différents contextes dans lesquels se sont déroulés les essais pris en considération par les calculs. Ici le terme interaction a son sens des essais thérapeutique et non pas celui des interactions pharmacologiques dans le cadre des associations de traitement. Il désigne les variables qui modifient la valeur de l’effet traitement, du risque relatif par exemple. Cette interaction est explorée dans les essais à l’aide des analyses en sous-groupes par exemple
Une covariable d’interaction est une variable rattachée aux patients, au contexte de l’essai ou aux modalités d’administration qui module l’efficacité du traitement, ce qui se traduit par une variation du risque relatif en fonction de la valeur de cette covariable. Ces interactions sont suspectées à l’aide des analyses en sous-groupes et plus particulièrement à l’aide du test d’interaction.
Le Tableau 5 donne un exemple d’interaction. L’effet du traitement A n’est vraisemblablement pas le même chez les diabétiques et chez les non diabétiques. Le risque relatif global de l’essai dépend alors de la répartition des patients entre diabétiques et non diabétiques.
Si, dans l’essai où est évalué le traitement B, la proportion de diabétiques est plus importante que celle existant dans l’essai du traitement A, la comparaison de A versus placebo dans les conditions de l’essai de B ne donnera pas le même risque relatif que celui dont on dispose à partir de l’essai de A réalisé.
Tableau 5 – Exemple d’une interaction entre l’effet du traitement (mesuré ici par le risque relatif) et une caractéristique patient (diabétique ou non diabétique)
|
|
Effectif |
Risque relatif Traitement vs placebo |
Interaction |
|
Essai
global |
1230 |
0.90 |
|
|
|
|
|
|
|
Diabétiques |
430 |
0.76 |
p=0.001 |
|
Non
diabétiques |
800 |
0.95 |
Faire le rapport des deux risques relatifs pose alors le problème de savoir de quels types de patients le RRa/b obtenu est alors représentatif : certainement pas représentatif des patients inclus dans l’essai B, vu que A n’aurait pas donné le risque relatif pris en compte pour le calcul chez ces patients (il y a moins de diabétiques dans l’essai à l’origine de l’estimation de RRa).
Si B n’est sujet à aucune interaction (il n’existe pas de variable modifiant son effet), sa comparaison contre placebo dans les conditions de l’essai de A aurait donné le même risque que celui dont on dispose. Le rapport RRa/RRb est alors valide pour la population étudiée dans l’essai de A et non pas pour la population des patient inclus dans l’essai de B.
Si les deux traitements sont sujets aux interactions, le rapport n’a plus de sens médical.
En pratique, écarter un problème de ce type nécessite de vérifier pour les deux traitements qu’aucune covariable ne modifie substantiellement l’effet des traitements. Cela s’effectue en regardant les tests d’interaction des analyses en sous-groupes. Mais le diagnostic peut être rendu difficile par le manque de puissance des tests d’interaction et par la possibilité que les variables pertinentes n’aient pas été analysées.
Par contre, les patients des essais versus placebo de A et de B ne sont pas nécessairement identiques en dehors de covariables d’interaction. En effet, s’ils diffèrent par leur risque d’événement (risque des groupes placebo des essais de A et de B), cette différence n’entrainera pas de modification de RRa ou RRb puisque que le risque relatif fait abstraction du niveau de risque de base (dans les groupes placebo) en calculant un rapport.
La situation problématique est bien représentée par les variables modulant le risque relatif. Il faut donc que les essais de A et de B soient similaires au niveau de ces covariables d’interaction. La difficulté vient du fait que les covariables d’interaction sont mal connues. Il faudra compter sur les analyses en sous-groupes réalisées dans les essais pour identifier les covariables d’interaction si elles existent et, le cas échéant, vérifier ensuite si la répartition de ces covariables est identique dans tous les essais (à l’aide des tableaux des caractéristiques de base).
Cependant, il s’avère que l’existence de covariables d’interaction forte est assez peu fréquente. A priori, il est relativement vraisemblable que les conditions de validité sont satisfaites à partir du moment où les essais de A et de B ont eu lieu dans des contextes proches (essais contemporains les uns des autres, disponibilité de traitements concomitants similaire) et avec des patients proches.
1.6 Utilisation de la méta-analyse
En pratique, on se retrouve confronté
à l’existence de plusieurs essais de A versus placebo et de B
versus placebo. Les calculs de comparaisons indirectes ajustées nécessitent
un seul risque relatif pour A et un seul pour B. Sélectionner un seul
essai de A et un seul de B introduirait un arbitraire inacceptable dans
Des plus, le caractère généralisable des résultats issus d’une méta-analyse est supérieur à celui des résultats issus d’une seule étude, puisque cette technique regroupe des études réalisées sur des populations différentes et avec des protocoles quelque peu différents.
Figure 1 – Utilisation de la méta-analyse pour le calcul des comparaisons indirectes ajustées.
1.1 Existence de plusieurs chemins et évaluation de l’incohérence
Dans certains cas, il s’avère que des comparaisons indirectes ajustées pourraient être réalisées à l’aide de plusieurs chemins et non pas seulement en passant par le placebo.
Le terme chemin désigne en fait le comparateur commun des comparaisons de base sur lesquelles s’appuie l’extrapolation effectuée par la comparaison indirecte ajustée.
Dans le cas simple que nous avons évoqué jusqu’à présent, la comparaison indirecte de A versus B s’effectue à l’aide du chemin Aà placebo à B puisque les deux comparaisons de bases utilisées sont versus placebo.
La comparaison indirecte de A et B peut aussi passer par un autre chemin si des essais de A et de B versus un autre comparateur commun sont disponibles. Par exemple, un ancien traitement actif C. La disponibilité d’essais A versus C et B versus D va permettre d’estimer A versus B par le chemin Aà C à B.
Les calculs vont donc donner deux estimations indépendantes de la comparaison indirecte de A versus B (celle passant par le placebo et celle passant par C). L’existence de ces deux résultats va permettre de tester s’il y a une incohérence entre ces deux chemins, c’est-à-dire si le résultat de la comparaison indirecte varie en fonction du chemin (cf. Figure 2). Ce test se base sur l’hétérogénéité entre les deux estimations produites du risque relatif A vs B : RRA/B et RR’A/B.
En cas hétérogénéité (c’est-à-dire s’il existe une différence statistiquement significative entre RRA/B et RR’A/B), il y a incohérence : le résultat varie en fonction du chemin. Cette situation est gênante car quelque soit le chemin, on devrait obtenir le même résultat et il conviendra d’émettre des réserves sur le résultat, sauf en cas d’explication claire et non arbitraire de l’incohérence.
En l’absence d’hétérogénéité, le résultat final sera la méta-analyse des deux estimations RRA/B et RR’A/B donnant la meilleure précision possible. L’absence d’incohérence détectée renforce la confiance que l’on peut avoir dans le résultat.
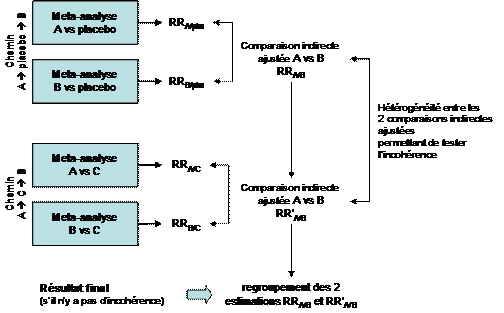
Figure 2 – Illustration du processus de comparaisons indirectes ajustées en cas d’existence de plusieurs chemins de comparaisons de base
1.2 Comparaisons de plus de deux traitements
En évaluation, il arrive fréquemment que la question posée soit de comparer simultanément plus de deux traitements concurrents.
A l’aide de la méthode des comparaisons indirectes ajustées, la comparaison de ces n traitements va nécessiter de procéder 2 à 2, étant donné que les comparaisons indirectes ajustées n’envisagent simultanément que deux traitements.
Pour 4 traitements T1, T2, T3 et T4 cela revient à faire 6 comparaisons :
· T1 vs T2
· T1 vs T3
· T1 vs T4
· T2 vs T3
· T2 vs T4
· T3 vs T4
Un problème de comparaisons multiples survient alors, entrainant une inflation du risque alpha. En effet, sous l’hypothèse nulle que tous les traitements ont la même efficacité (c’est-à-dire qu’il n’existe aucune différence entre les traitements pris 2 à 2), il y a pourtant 6 façons d’en trouver une du fait du seul hasard (les 6 comparaisons 2 à 2). Si chaque comparaison unitaire est réalisée avec un risque alpha de 5%, le risque global de trouver à tort au moins une différence entre les 4 traitements est fortement majoré et s’élève à 26%. Nous avons une chance sur quatre de conclure à l’existence d’un traitement plus efficace que les autres alors qu’en réalité ils sont tous aussi efficaces.
Ainsi, les comparaisons indirectes ajustées ont l’avantage d’un principe simple, facile à mettre en œuvre et facilement compréhensible. Par contre, cette méthode présente assez rapidement des limites lorsque la question posée englobe plus de deux traitements. D’autres méthodes n’ayant pas de limitations dans ce cas ont été développées. Il s’agit des méthodes basées sur une modélisation comme la méta-analyse en réseau, la méta-régression, etc…
2 L’approche mixte des comparaisons indirectes et directes
2.1 Principes
Les comparaisons indirectes peuvent conserver de l’intérêt même en cas de disponibilité d’essais de comparaisons directes.
En effet, souvent, l’essai de comparaison directe est unique. Assez fréquemment il a été conçu avec un manque manifeste de puissance. Dans d’autres cas, les modalités d’utilisation du comparateur sont discutables. Dans ces situations, la confrontation des résultats des comparaisons indirectes à celui de la comparaison directe présente un réel intérêt, celui de lever ou confirmer les réserves que l’on s’apprête à faire sur l’essai de comparaison directe.
L’approche mixte où l’on regroupe les résultats des comparaisons directes avec ceux des comparaisons directes est appelée « mixed treatment comparison ». Aucune terminologie stabilisée n’existe en Français pour l’instant.
En plus de ceux évoqués, cette approche mixte présente d’autres intérêts :
1. apprécier la validité des résultats de la comparaison indirecte ajustée
2. en cas de concordance des comparaisons directe et indirecte, combiner les résultats pour donner une estimation globale de la différence d’effet entre A et B tenant compte de la totalité de l’information disponible
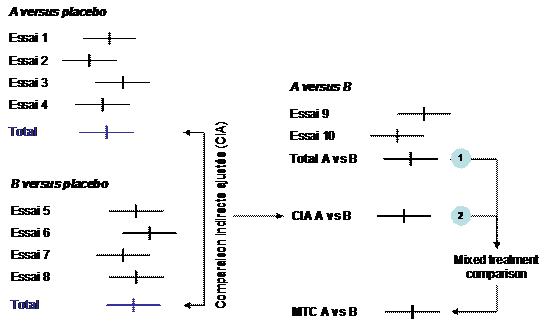
Figure 3 – Illustration du processus de Mixed Treatment Comparison (MTC). Le résultat de la méta-analyse des essais de comparaison directe (1) est combiné avec celui des comparaisons indirectes (2). La concordance de ces 2 estimations est testée par un test d’hétérogénéité
2.2 Exemple
Le regroupement des estimations issues des comparaisons indirectes ajustées avec celles des comparaisons directes s’effectue simplement par méta-analyse.
Song et al. (2) donne deux exemples de l’application de cette technique issus des publications faites par Soo et al. (3) et Trindade et al. (4) où, l’estimation des comparaisons directes étant en parfaite phase avec celle issue des comparaisons indirectes, la meilleure estimation possible est celle qui combine les résultats des deux approches (Figure 4).
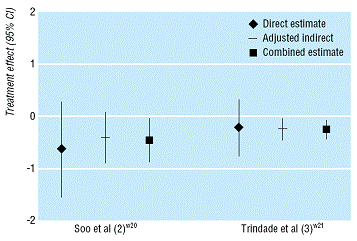
Figure 4 – Deux exemples
d’intégration par méta-analyse des résultats des
comparaisons directes avec ceux issus des comparaisons indirectes
ajustées
((2))
3 Les méthodes basées sur une estimation globale d’un réseau d’essais
3.1 Principe du réseau d’essais
L’idée générale de cette approche est de représenter l’ensemble de l’information apporté par les divers essais du domaine sous la forme d’un réseau (« Network of evidence »). Dans ce réseau, les sommets (les points) représentent les traitements et les flèches reliant les sommets représentent les comparaisons disponibles (effectuées par des essais comparant les traitements situés de part et d’autre de la flèche, le sens de la flèche donnant le sens de la comparaison et des risques relatifs). La Figure 7 donne un exemple d’un tel réseau issu de la méta-analyse des traitements anti hypertenseurs publiée en 2007 par Elliot et col. (5). Cette méta-analyse s’intéressait à l’apparition du diabète avec les traitements antihypertenseurs.
Les méthodes d’estimation globale proposées (cf. section 3.1.4) permettent alors d’estimer l’efficacité de tous les traitements par rapport à un traitement de référence choisi arbitrairement ou non. Les résultats sont représentés sous forme de graphiques classiques de méta-analyse, directement compréhensibles (cf. Figure 6).
L’estimation est globale, utilisant les comparaisons directes existantes aussi bien que les comparaisons indirectes réalisables. La hiérarchie est établie de manière quantitative à partir de l’estimation des tailles d’effet ce qui la met à l’abri des problèmes liés à la non transitivité des tests statistiques (cf. §Erreur ! Source du renvoi introuvable.).
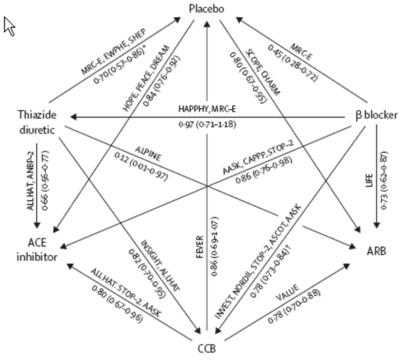
Figure 5 – Réseaux des essais d’antihypertenseurs dans lesquels l’incidence du diabète est rapportée. Les comparaisons directes disponibles sont représentées par les flèches avec indications des noms des essais, de l’odds ratio et de son intervalle de confiance.
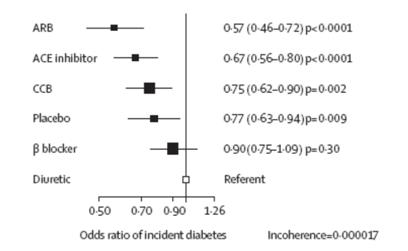
Figure 6 – Résultats de la méta-analyse en réseau sur le critère « apparition du diabète »
Attention l’interprétation de ce graphique à la recherche du traitement induisant le moins de cas incidents de diabète revient à faire une comparaison indirecte naïve. En effet, si à l’issu de l’analyse de ce graphe, on considère les sartans (ARB) supérieurs aux IEC (ACE inhibitor) parce que l’odds ratio sartan versus diurétique est plus intéressant que l’odds ratio IEC versus diurétique, on effectue une simple comparaison naïve des odds ratio. L’interprétation correct de ce graphique doit se limiter à : « Cette méta-analyse en réseau montre que le placebo, les antagonistes calciques (CCB), les IEC et les sartans (ARB) entrainent moins de cas incidents de diabète que les diurétiques ». Aucune conclusion n’est possible pour les bétabloquants.
3.2 La notion d’incohérence
Le réseau le plus simple est celui qui
concerne seulement deux traitements A et B (Figure 7). La valeur figurant à
côté de la flèche est l’estimation de l’effet
de B par rapport à A. Dans la suite de la présentation, nous
considérerons que l’estimation de l’effet est effectuée
par la différence (de risque par exemple) désignée par dAB :
où xA
et xB désignent les
valeurs obtenues dans les bras A et B de
|
Figure 7 – Réseau impliquant seulement 2 traitements A et B |
|
Dans une situation où deux comparaisons sont disponibles, celle de C par rapport à A et celle de B par rapport à C, on obtient le réseau représenté sur la Figure 8.
|
Figure 8 –Réseau comprenant 2 types de comparaisons C versus A et B versus C |
|
Un moyen simple d’obtenir l’effet de B par rapport à A est de faire la somme
Soit, avec les valeurs numériques de l’exemple de la Figure 8, dAB = 0.6+0.5 = 1.1.
Si 4 types de comparaisons sont disponibles, le graphe du réseau de ces résultats prend la forme représentée Figure 9.
|
Figure 9 – Réseau de 4 traitements |
|
La même différence dAB
peut maintenant être obtenue par deux chemins différents : A à
C à
B et A à
D à
B. dAB
est obtenu par pour le premier
chemin et par 
pour le second,
soit avec les valeurs numériques :
0.4 + 0.6 = 1.0 et 0.6 + 0.5 = 1.1. Ainsi,
on obtient deux estimations de dAB très proches l’une de
l’autre quel que soit le chemin de comparaison suivi. Une certaine
cohérence existe dans le réseau de comparaisons indirectes
possibles.
Dans la situation illustrée par la Figure 10, le premier chemin donne comme estimation de dAB -0.6-0.4 = -1.0 et le second 0.5+0.6=1.1. Ici, il y a une complète discordance entre les deux estimations traduisant une incohérence dans le réseau de comparaisons. Aucune estimation indirecte de A versus B ne sera possible. Cette notion d’incohérence est donc un élément important de la validité des comparaisons indirectes (réalisées à travers un réseau de comparaisons). Si elle est testable, c’est-à-dire si plusieurs chemins existent pour effectuer la même extrapolation, son absence est un élément confortant la validité des extrapolations obtenues : quelque soit la façon de procéder, la même estimation est obtenue.
|
Figure 10 – Exemple d’incohérence dans un réseau de comparaisons |
|
3.3
Les réseaux de comparaisons
correspondant aux différents schémas de développement
Les différents schémas de développement évoqués dans les section Erreur ! Source du renvoi introuvable. et Erreur ! Source du renvoi introuvable. peuvent être illustrés à l’aide de réseaux de comparaisons.
Le réseau présenté Figure 11 correspond à une situation où tous les traitements concurrents ont été développés à l’aide d’essais versus placebo.
|
Figure 11 – Réseau d’évaluation de tous les traitements concurrents contre placebo |
|
Le réseau de la Figure 12 correspond à une situation où le recours au placebo est impossible à partir du moment où un traitement efficace est disponible (évaluation de traitements visant à réduire la mortalité par exemple). Les essais utilisent comme contrôle le dernier traitement ayant montré sa supériorité.
|
Figure 12 – Réseau où le recours au placebo est impossible à partir du moment où un traitement efficace est disponible |
|
3.4
Les méthodes
d’estimation proposées pour les réseaux
d’essais
Plusieurs modèles ont été proposés dans la littérature pour représenter des réseaux. Plusieurs méthodes statistiques pour l’estimation des paramètres de ces modèles (en particulier ceux caractérisant les comparaisons de traitements) ont aussi été proposées. Cette diversité débouche sur la classification suivante :
·
Utilisation de
méthodes Bayesiennes : Bayesian network meta-analysis
o Mixed Treatment Comparison par Lu et Ades (6)
o Modèle de Cadwell de « mixed treatment comparison »
· Estimation à l’aide d’un modèle linéaire mixte
o Network meta-analysis de Lumley (7)
4 « Bayesian network meta-analysis »
Parmi les différents modèles proposés pour réaliser des méta-analyses bayésiennes en réseau (Bayesian network meta-analysis), le plus abouti semble être celui proposé par Lu et Ades (6). Il découle des précédents modèles proposés par Cadwell (cf. infra), et Smith, Spiegelhalter et Thomas(9). Tous ces modèles reposent sur la proposition de méta-analyses Bayesiennes faite par Higgins et Whitehead (10).
La mise en œuvre des ces méthodes fait appel à des techniques d’intégration par Monte Carlo des chaines de Markov à l’aide du logiciel Winbugs.
4.1 Modèle de Lu et Ades
4.1.1 Méthode statistique
Lu et Ades (6) propose une extension à I traitements du modèle de Smith-Spiegelhalter-Thomas(9) pour combiner comparaisons directes et indirectes afin de réaliser des « mixed treatment comparisons ». Leur modèle prend aussi en compte naturellement les essais multibras qui posent le problème de la non indépendance (corrélation) des comparaisons réalisées avec un contrôle commun. L’estimation est réalisée par une approche Bayesienne implémentée à l’aide des techniques de Monte Carlo sur Chaine de Markov.
Le modèle de base à deux traitements ne s’applique qu’aux critères de jugement binaires et se construit de la façon suivante.
Les exposants T
et C désignent respectivement le
traitement étudié T et le
traitement contrôle C.
L’indice k désigne le k-ème essais. r est le nombre
d’événements observés dans un groupe de taille n, p est la
probabilité de survenue de l’événement.
L’effet du traitement 
est
autorisé à varier d’un essai à l’autre. Il
s’agit donc d’un modèle de méta-analyse
aléatoire. L’effet global du traitement (en temps que méta-paramètre)
est estimé par d. Au niveau de
chaque essai, 
désigne la
fréquence moyenne d’événement dans les groupes T et C qui,
n’étant pas un paramètre d’intérêt, est
traitée comme un paramètre de nuisance.
Avec ces conventions, le modèle est
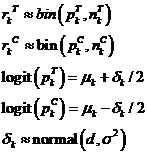
L’intérêt de ce modèle est qu’il peut être facilement généralisé à des essais multibras. L’extension à I traitements i, s’effectue par :
|
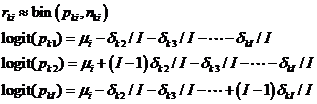
Encadré - Méthodes de Monte
Carlo par chaînes de Markov (MCMC) |
|
Les
méthodes de Monte Carlo par chaînes de Markov (MCMC) permettent,
pour un paramètre d’intérêt, d’obtenir sa
distribution à partir des données observées. D’une
manière simplifiée, la distribution d’une variable
aléatoire donne la probabilité d’une que le
paramètre prennent une valeur particulière. L’observation
de la distribution permet de déterminer la valeur « la plus
probable », c'est-à-dire le sommet de Si l’on connaissait parfaitement la valeur du paramètre que l’on cherche à estimer, la distribution serait un trait vertical. Une seule valeur à une probabilité de 100%, toutes les autres une probabilité de 0% d’être la vraie valeur du paramètre estimé. En pratique cela n’est jamais le cas, et l’étalement de la distribution traduit l’imprécision avec laquelle on connait la vraie valeur. La distribution du paramètre que l’on cherche à estimer est déterminée à partir des données observée (comme tout procédé d’estimation). Cependant les méthodes Bayesiennes ont un prix à payer qui est celui de nécessité une hypothèse a priori sur la distribution du paramètre. Le résultat produit, la distribution estimée du paramètre, dépend donc à la fois des données et de l’a priori qui a été choisi. Ces méthodes donne une distribution a posteriori (c'est-à-dire après l’observation des données) à partir d’une distribution a priori (telle que on l’imagine a priori, avant d’obtenir toute information par les données). La nécessité de donner une distribution a priori de l’élément que l’on ignore et que l’on cherche à connaitre à travers l’observation est la principale difficulté de cette approche. Ce point est important, car bien entendu le résultat (la distribution a posteriori estimée) peut changer fortement en fonction de l’a priori qui est fixé. Heureusement, il est possible de trouver des a priori « non informatif », c'est-à-dire qui n’introduisent que très peu d’information. Ainsi, ces a priori ne conditionnent pas le résultat. Ces distributions a priori non-informatives disent en quelque sorte, qu’a priori (c'est-à-dire avant d’observer la première donnée), toute valeur est possible pour la vraie valeur du paramètre et qu’il n’est donc pas justifié d’en favoriser une plus qu’une autre. L’obtention de la distribution a
posteriori à partir de la distribution a priori s’effectue a
l’aide du théorème de Bayes,
d’où le nom de méthode Bayesienne. Le
théorème de Bayes spécifie que la distribution a
posteriori Avec Avec les techniques de MCMC, la transformation à l’aide de l’information apportées par les données de la distribution a priori pour obtenir la distribution a posteriori ne va pas se faire de façon analytique (à l’aide de formule) mais en recourant au calcul intensif grâce à un ordinateur. L’estimation de la valeur du paramètre q du modèle s’effectue en répétant en boucle le même processus un très grand nombre de fois jusqu’à l’obtention d’une stabilisation de l’estimation de la distribution. Le processus d’estimation consiste à produire à l’aide de génération de nombres aléatoires une distribution a posteriori à partir d’une distribution a priori et des données. La distribution a posteriori obtenue devient la distribution a priori de la boucle suivante, et ainsi de suite. Un théorème assure la convergence du processus vers la vraie distribution a posteriori du paramètre à estimer. Le processus produit donc une séquence (chaine) de nombres qui après exclusion des premières valeurs (burn-in) représente un échantillon aléatoire de la distribution a posteriori. L’analyse descriptive de cette séquence (moyenne, médiane, quantile, représentation de l’histogramme) permet d’estimer de manière empirique la distribution du paramètre d’intérêt. Au total, l’utilisation de ces
techniques utilise en entrée : les données
observées, une distribution a priori et la première valeur du
paramètre. En sortie est produite une longue séquence de nombre
(chaine de Markov) dont la partie finale est une estimation empirique de |
4.2
Modèle de Cadwell
4.2.1 Méthode statistique
Le modèle proposé par Cadwell (11) est une généralisation de celui proposé par Higgins et Whitehead (10).
Soit une méta-analyse où k traitements ont été comparés entre eux dans les essais. Pour chaque essai j, soit rjk le nombre d’événements observés dans le bras du traitement k dont l’effectif est njk.
Le nombre d’événements suit une distribution binomiale
où pjk est la fréquence (le risque) de survenue de l’événement, critère de jugement.
L’utilisation d’un odds ratio pour représenter les effets traitement revient à modéliser des logit de la façon suivante :
lorsque k=b, b désignant
le traitement de référence aux comparaisons
et 
quand k est différent de b.
µjb représente en quelque sorte une valeur de base de l’odds du critère de jugement dans l’essai j.
Ce modèle peut être décliné en deux variantes reposant soit sur un modèle fixe des effets soit sur un modèle d’effets aléatoires. L’estimation s’effectue par MCMC à l’aide du logiciel Winbugs par exemple et nécessite l’introduction dans le processus d’estimation de distributions a-priori non informatives.
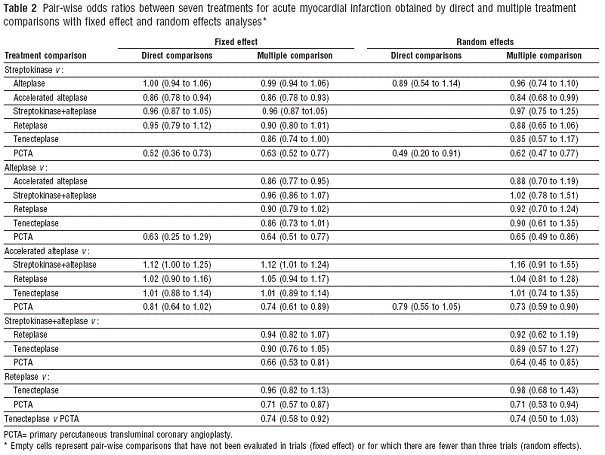
Cette approche à par exemple était utilisé pour comparer les fibrinolytique à la phase aigue de l’infarctus (Figure 13) (11).
Tableau 6 – Application de la méthode proposé par Cadwell et al. aux fibrinolytiques à la phase aiguë de l’infarctus du myocarde ((11))
5 Estimation à l’aide d’un modèle linéaire mixte
5.1.1 Méthode statistique
L’utilisation d’un modèle linéaire mixte pour la réalisation des comparaisons indirectes à travers un réseau de comparaison a été proposée en 2002 par Thomas Lumley (7).
L’effet traitement estimé
à partir de l’essai k comparant les
traitements i et j est
noté 
avec comme
variance estimée 
.
Le modèle des comporte trois
composantes en plus de l’erreur d’échantillonnage :
1.
le méta vrai effet des
traitements i et j qui est
désigné par 
et 
respectivement.
Le méta vrai effet est la valeur autour de laquelle fluctuent les vrais
effets traitement développés dans chaque essai. L’effet
observé provient du vrai effet plus ou moins entaché de
l’erreur d’échantillonnage (liée à la
fluctuation d’échantillonnage).
2.
l’effet aléatoire 
et 
qui
représente la différence entre le vrai effet traitement de
l’essai k et les méta-valeurs
correspondantes et ont comme
variance 
. Le vrai effet du traitement i
dans l’essai k est donc 
. est
l’estimation de la différence entre les traitements i et j dans
l’essai k, c’est donc une
estimation de la différence entre les vraies effets et 
.
3.
un second effet aléatoire 
représentant le changement de
l’effet du traitement i quand il est
comparé à j. permet ainsi de
capter l’incohérence éventuelle du réseau
d’évidence. Sa variance 
permet de mesurer
l’incohérence du réseau.
Au total, le modèle est donc
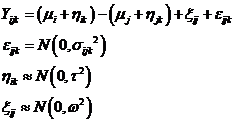
Où 
désigne
l’erreur aléatoire d’échantillonnage qui entache au
niveau de l’essai k
l’estimation de la différence entre le traitement i et le traitement j.
|
Encart – Modèle mixte,
hiérarchique |
|
En statistique, un effet est la modification qu’induit un facteur dans la valeur d’une variable aléatoire. Dans un essai, le facteur traitement entraîne une modification dans la valeur de la variable utilisée comme critère de jugement. La plupart du temps, les facteurs sont considérés comme étant fixes. L’effet traitement est donc la modification constante qu’induit en moyenne le traitement sur la variable aléatoire utilisée comme critère de jugement. Les modèles à effets mixtes, appelés aussi modèles à effets aléatoires, permettent de prendre en compte plusieurs niveaux de fluctuation/erreur aléatoires (les effets aléatoires) et ainsi de considérer que des effets peuvent varier aussi de manière aléatoire. La qualification aléatoire de l’effet signifie que cet effet varie d’une unité statistique à l’autre, de manière aléatoire suivant une certaine distribution. En méta-analyse, la modélisation à l’aide d’un modèle fixe représente la réalité en considérant que l’effet Y observé dans l’essai k est égal au vrai effet traitement, plus les fluctuations aléatoires d’échantillonnage (c’est-à-dire l’erreur aléatoire se produisant au niveau de l’essai entre la valeur observée et la vraie valeur). Dans ce modèle, il n’y a donc qu’un seul effet (le vrai effet du traitement) et qui est fixe pour tous les essais (d’où le nom de modèle à effet fixe). Un modèle aléatoire de méta-analyse stipulera que le vrai effet du traitement est variable d’un essai à l’autre en fluctuant de manière aléatoire autour d’une valeur qui est un méta-paramètre. L’effet qui est recherché au niveau de l’essai n’est donc plus fixe mais aléatoire, d’où le nom de modèle à effet aléatoire. La méta-analyse cherche alors à estimer le méta-paramètre. Ce modèle stipule donc une hétérogénéité de l’effet du traitement (l’effet varie d’un essai à l’autre de manière aléatoire). Dans ce modèle aléatoire, nous avons donc deux niveaux de variabilité dûe au hasard : 1. les fluctuations d’échantillonnage (comme avec le modèle fixe) décrivant la différence entre la vraie valeur de l’effet traitement dans un essai et l’effet observé 2. les fluctuations du vrai effet entre les essais |
5.1.2 Exemple d’application
Cette méthode a été employée dans la méta-analyse de Psaty sur les antihypertenseurs de première ligne (8). L’objectif était de compléter et d’estimer toutes les comparaisons possibles du réseau de la Figure 13. Par exemple, aucun essai ne compare directement les Low-dose diuretics aux Angiotensin receptor blockers. La comparaison indirecte réalisée de manière implicite par la méthode permet cependant de la documenter comme le montrent les résultats produits Figure 13, sous figure E).
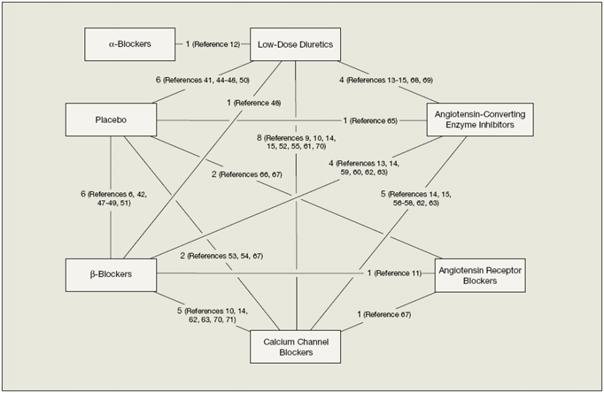
Figure 13 – Réseau de comparaisons pris en compte ((8))
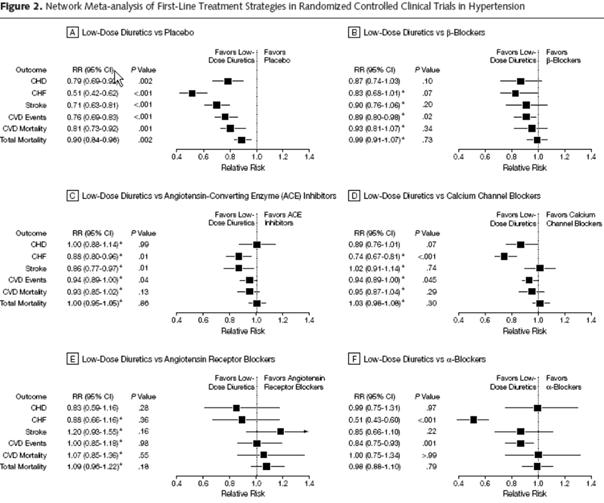
Figure 14 – Résultats de la méta-analyse en réseau ((8))
6 Méta-régression
6.1 Généralités
Une autre méthode utilisable pour réaliser des comparaisons indirectes de traitement est la méta-régression.
La méta-régression est une technique standard de méta-analyse qui consiste à modéliser l’effet observé dans les essais à l’aide de covariables (12-16). Il s’agit souvent d’une régression linéaire avec comme variable à expliquer l’effet (ou une de ses transformations) et comme variables explicatives des covariables décrivant les traitements évalués (dose, molécules, ...), les patients inclus dans les essais, les caractéristiques méthodologies des essais, etc…
La méta-régression a par exemple été utilisée pour rechercher s’il existait une relation entre la réduction de morbi-mortalité apportée par les statines et l’intensité de la baisse du LDL obtenue (17).
Pour des raisons statistiques, il est préférable d’utiliser le logarithme de l’odds ratio comme mesure de l’effet du traitement. Le modèle de méta-régression s’écrit alors :
où ORi désigne l’odds ratio
mesuré dans l’essai i, x1,i la valeur de la covariable 1 dans cet essai i, etc. pour toutes covariables prises en
considération. ei représente le résidu
aléatoire qui est considéré comme distribué
normalement avec comme variance résiduelle s2.
ei représente ainsi la part de la
variance de l’effet entre études non expliquée par les
covariables considérées.
L’estimation
des coefficients b1, b2, … peut s’effectuer par
différentes méthodes d’ajustement comme les moindres
carrés, les moindres carrés pondérés, etc...
Thompson recommande cependant d’utiliser la méthode du maximum de
vraisemblance restreinte (REML) (15).
Un
modèle aléatoire peut aussi être utilisé. En
estimant simultanément plusieurs comparaisons indirectes, la
méta-régression s’apparente aussi aux méthodes
basées sur la modélisation d’un réseau
d’essais.
6.2 Méta-régression et effet traitement fixe
6.2.1 Modèle
L’utilisation de la technique de méta-régression pour faire des comparaisons indirectes s’effectue en codant les traitements à comparer à l’aide des covariables.
Considérons une situations où 3 traitements A,B,C ont donnés lieux à une série d’essais contre placebo. La réalisation des comparaisons indirectes de l’efficacité de ces 3 traitements s’effectuera en ajustant sur les données fournies par ces séries d’essais le modèle suivant :
Le codage du traitement évalué est effectué à l’aide de deux covariables X1 et X2 (technique des dummy variable) en prenant le traitement A comme référence :
|
Essais |
X1 |
X2 |
|
A versus placebo |
0 |
0 |
|
B versus placebo |
1 |
0 |
|
C versus placebo |
0 |
1 |
Ainsi, le coefficient b1 estimera l’effet de B par rapport à A et le coefficient b2 celui de C par rapport à A. Tout autre traitement aurait put être pris comme référence bien entendu.
En effet, pour le traitement A (soit x1=0 et x2=0) on a
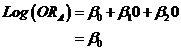
Et pour le traitement B
Ainsi
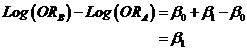
Comme
, on a
Or 
, l’odds ratio de B par rapport à A. En
effet :
De même
Ce qui donne
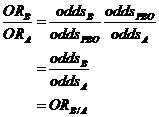
Au total on a donc
ORB/A = exp(b1) et ORC/A=exp(b2)
La méta-régression permet aussi de faire des tests statistiques. Ainsi pour s’avoir si B est statistiquement différent de A il suffit de tester l’hypothèse b1=0. De même, l’estimation de l’odds ratio de B/A est assortie de son intervalle de confiance.
6.2.2 Exemple d’utilisation
La méta-régression avec un modèle à effet mixte a par exemple été utilisée par Eckert pour comparer la duloxetine à la fluoxetine et à la venlafaxine (18)
6.3 Méta-regression et effet traitement aléatoire (méthode Bayesienne)
Nixon, Bansback, et Brennan propose une implémentation de la méta-régression pour faire des mixed treatment comparison à l’aide d’un modèle Bayesien estimé par MCMC (19). Par rapport à la méta-régression simple, leur modèle inclus un effet traitement aléatoire et améliore ses performances en ajustant sur des covariables.
7 Méthodes pour les critères de jugement continus
Les méthodes proposées jusqu’à présent ne s’appliquent qu’aux critères de jugement binaires. Parmi ces méthodes, une seule est directement transposable aux critères continus : celle des comparaisons indirectes ajustées. Il suffit de remplacer le risque relatif par une mesure adaptée à la méta-analyse des critères continus, la différence pondérée des moyennes (weighted mean difference, WMD) ou l’ampleur d’effet (effect size).
Par contre, l’approche par « evidence network » n’offre pas de transposition directe aux critères continus et va nécessiter des développements spécifiques.
La méta-analyse de Packer et al. comparant carvédilol et métoprolol sur la fraction d’éjection ventriculaire dans l’insuffisance cardiaque donne un exemple d’utilisation des comparaisons indirectes ajustées avec un critère de jugement continu (20).
8 Comparaison des différentes méthodes
Il existe un seul travail ayant comparé les performances statistiques de ces différentes méthodes. Glenny et al. montrent (chapitre 5) en utilisant les données de l’essai IST (International Stroke trial) pour créer des pseudo essais que ces différentes méthodes produisent des estimations très proches les unes des autres (1). Les méthodes qu’ils ont comparées sont les suivantes :
· Comparaison indirecte ajustée à l’aide d’un modèle fixe
· Comparaison indirecte ajustée à l’aide d’un modèle aléatoire (DerSimonian et Laird)
· Régression logistique
· Méta-régression à effet aléatoire
· Méthode naïve par comparaison des bras
Les
résultats montrent qu’avec ces données, toutes les
méthodes donnent des estimations ponctuelles très voisines les
unes des autres. Cependant, pour l’estimation des erreurs standard (et
donc pour la réalisation des tests statistiques), étant
donné l’existence d’au moins trois niveaux de
variabilité dans la question posée par les comparaisons
indirectes, les méthodes basées sur un modèle
aléatoire semblent plus raisonnables.
Le Tableau 7 tente de comparer les avantages et les inconvénients théoriques des différentes méthodes.
A coté des aspects statistiques, il convient aussi de noter que seules les comparaisons indirectes ajustées ont fait l’objet d’une étude empirique de leur validité par comparaison de leurs résultats à ceux des comparaisons directes (cf. chapitre Erreur ! Source du renvoi introuvable.). De plus, il s’agit de la seule méthode qui puisse donner des résultats en utilisant le risque relatif. Les autres approches conduisent à des odds ratio. Bien que l’odds ratio ait de bonnes propriétés mathématiques et statistiques, son interprétation reste difficile. Le risque relatif est d’un abord intuitif et semble de ce fait plus adapté pour les questions d’évaluation thérapeutique et les méta-analyses (21).
Au total, en l’absence de différence connue dans les performances des différentes méthodes, il est difficile de recommander une méthode plus qu’une autre. Deux approches cependant peuvent être mises en avant :
1. les comparaisons indirectes ajustées, en raison de leur simplicité, de leur transparence (l’origine des résultats mis en avant est claire), de la possibilité d’exprimer les résultats en risque relatif et qu’il s’agit de la seule méthode disponible en standard en cas de critère continu ;
2. les méthodes Bayesiennes basées sur un réseau (evidence network) en raison de la grande flexibilité du modèle (permettant une modélisation fine et souple des données, adaptable à des cas particuliers), de l’estimation de l’incohérence, de la prise en compte des essais multibras.
Tableau 7 – Comparaison des avantages et inconvénients théoriques des différentes méthodes
|
Méthode |
Avantages |
Inconvénients / limites |
|
Comparaison indirecte ajustée (Adjusted indirect comparison) |
· Simplicité des calculs · Transparence · Utilisable avec le risque relatif · Transposable aux critères
continus · Validation empirique de la concordance
des comparaisons indirectes par rapports aux comparaisons directes |
· Impossibilité de tester
l’incohérence · Conduit à la réalisation
de comparaisons deux à deux en cas de plus de 2 traitements à
comparer |
|
Méta-régression |
· Ajustement sur d’autres
covariables introduisant de
l’hétérogénéité · Ne nécessite pas forcément
de MCMC · Mais estimable aussi par MCMC |
· Pas d’estimation de
l’incohérence · Donne des odds ratio · Pas d’étude empirique de
validité |
|
Méthodes basées
sur les « evidence network » |
||
|
Lumley |
· Test de l’incohérence · Ne nécessite pas de MCMC |
· Pas d’étude empirique de
validité · Donne des odds ratio |
|
Lu |
· Test de l’incohérence · Prise en compte des essais multibras · Possibilité d’utiliser un
modèle aléatoire |
· Méthode d’estimation
délicate requérant un haut degré d’expertise (analyse
de la convergence entre autres) · Approche Bayesienne donc
nécessitant l’introduction d’information a priori · Pas d’étude empirique de
validité · Donne des odds ratio · |
|
Cadwell |
· Test de l’incohérence · Prise en compte des essais multibras · Possibilité d’utiliser un
modèle aléatoire |
· Méthode d’estimation
délicate requérant un haut degré d’expertise
(analyse de la convergence entre autres) · Approche Bayesienne donc
nécessitant l’introduction d’information a priori · Pas d’étude empirique de
validité · Donne des odds ratio |
|
MCMC : Monte Carlo Markov Chain |
||
9 Références
1. Glenny AM, Altman DG, Song F, Sakarovitch C, Deeks JJ, D'Amico R, et al. Indirect comparisons of competing interventions. Health Technol Assess 2005;9(26):1-134, iii-iv.
2. Song F, Altman DG, Glenny AM, Deeks JJ. Validity of indirect comparison for estimating efficacy of competing interventions: empirical evidence from published meta-analyses. Bmj 2003;326(7387):472.
3. Soo S, Moayyedi P, Deeks J, Delaney B, Innes M, Forman D. Pharmacological interventions for non-ulcer dyspepsia. Cochrane Database Syst Rev 2000(2):CD001960.
4. Trindade E, Menon D. Selective serotonin reuptake inhibitors (SSRIs) for major depression. Part I. Evaluation of the clinical literature. Ottawa, ON: Canadian Coordinating Office for Health Technology Assessment.; 1997.
5. Elliott WJ, Meyer PM. Incident diabetes in clinical trials of antihypertensive drugs: a network meta-analysis. Lancet 2007;369(9557):201-7.
6. Lu G, Ades AE. Combination of direct and indirect evidence in mixed treatment comparisons. Stat Med 2004;23(20):3105-24.
7. Lumley T. Network meta-analysis for indirect treatment comparisons. Stat Med 2002;21(16):2313-24.
8. Psaty BM, Lumley T, Furberg CD, Schellenbaum G, Pahor M, Alderman MH, et al. Health outcomes associated with various antihypertensive therapies used as first-line agents: a network meta-analysis. Jama 2003;289(19):2534-44.
9. Smith TC, Spiegelhalter DJ, Thomas A. Bayesian approaches to random-effects meta-analysis: a comparative study. Stat Med 1995;14(24):2685-99.
10. Higgins JP, Whitehead A. Borrowing strength from external trials in a meta-analysis. Stat Med 1996;15(24):2733-49.
11. Caldwell DM, Ades AE, Higgins JP. Simultaneous comparison of multiple treatments: combining direct and indirect evidence. Bmj 2005;331(7521):897-900.
12. Higgins JP, Thompson SG. Controlling the risk of spurious findings from meta-regression. Stat Med 2004;23(11):1663-82.
13. Teramukai S, Matsuyama Y, Mizuno S, Sakamoto J. Individual patient-level and study-level meta-analysis for investigating modifiers of treatment effect. Jpn J Clin Oncol 2004;34(12):717-21.
14. Thompson SG, Higgins JP. How should meta-regression analyses be undertaken and interpreted? Stat Med 2002;21(11):1559-73.
15. Thompson SG, Sharp SJ. Explaining heterogeneity in meta-analysis: a comparison of methods. Stat Med 1999;18(20):2693-708.
16. van Houwelingen HC, Arends LR, Stijnen T. Advanced methods in meta-analysis: multivariate approach and meta-regression. Stat Med 2002;21(4):589-624.
17. Baigent C, Keech A, Kearney PM, Blackwell L, Buck G, Pollicino C, et al. Efficacy and safety of cholesterol-lowering treatment: prospective meta-analysis of data from 90,056 participants in 14 randomised trials of statins. Lancet 2005;366(9493):1267-78.
18. Eckert L, Lancon C. Duloxetine compared with fluoxetine and venlafaxine: use of meta-regression analysis for indirect comparisons. BMC Psychiatry 2006;6:30.
19. Nixon RM, Bansback N, Brennan A. Using mixed treatment comparisons and meta-regression to perform indirect comparisons to estimate the efficacy of biologic treatments in rheumatoid arthritis. Stat Med 2007;26(6):1237-54.
20. Packer M, Antonopoulos GV, Berlin JA, Chittams J, Konstam MA, Udelson JE. Comparative effects of carvedilol and metoprolol on left ventricular ejection fraction in heart failure: results of a meta-analysis. Am Heart J 2001;141(6):899-907.
21. Deeks JJ. Issues in the selection of a summary statistic for meta-analysis of clinical trials with binary outcomes. Stat Med 2002;21(11):1575-600.
Interprétation
des essais cliniques pour la pratique médicale
www.spc.univ-lyon1.fr/polycop
Faculté de Médecine Lyon - Laennec
Mis à jour : aout 2009