Biais de publication
Accueil > Sommaire > Analyse ajustée
Le biais de publication a été formalisé à l'occasion du développement des techniques de méta-analyses, mais ce biais n'est pas spécifique de cette approche. Il touche en fait toute action récapitulative des résultats de la recherche (personnelle, revue de la littérature, méta-analyse). Par contre, contrairement aux autres méthodes, la méta-analyse donne des moyens de rechercher le biais de publication : funnel plot ,calcul de la robustesse, etc.
1 Définition
Toute synthèse d’information est sujette à un biais qui lui est propre : le biais de publication (« publication bias »).
Les résultats négatifs (essais ne montrant pas de différence significative) sont moins fréquemment publiés que les résultats positifs (essais montrant une différence significative). L'étude du devenir de 285 protocoles soumis au comité d'éthique d'Oxford révèle que 85% des résultats positifs ont été publiés contre seulement 56% des résultats négatifs [1]. Il existe ainsi une publication sélective des résultats positifs au détriment des résultats négatifs. Cela ne veut pas dire que ces derniers ne sont jamais publiés mais plus difficilement et seulement pour une partie d'entre eux.
Les causes de ce phénomène sont certainement nombreuses [2, 3] et impliquent à la fois les comités de lecture des revues, peu séduits par un résultat négatif, et les auteurs qui n'investissent pas dans la rédaction d'un article qui a peu de chance d'être accepté.
Ce phénomène de publication sélective va fausser les conclusions que l'on peut tirer à partir des résultats publiés. C'est le biais de publication. Dans une synthèse, si aucune recherche poussée des essais non publiés n'est entreprise, le risque couru est de ne travailler qu'avec les essais positifs, ce qui conduit à une surestimation de l'efficacité du traitement.
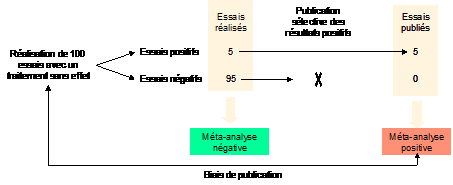
Figure 1 – Si de nombreux essais sont réalisés avec un traitement sans efficacité, certains d'entre eux auront cependant un résultat statistiquement significatif, uniquement du fait du risque d'erreur statistique alpha que l'on consent au niveau du test statistique. Ainsi, si 100 essais sont réalisés, 5 d'entre eux seront positifs à tort, du fait du hasard. Ainsi, si uniquement les essais positifs sont publiés, une synthèse ne portant que sur les résultats publiés donnera une fausse impression d'efficacité du traitement. C'est le biais de publication.
Les conséquences potentiellement dommageables du biais de publication sont illustrées par l’exemple des antiarythmiques de classe 1 en post infarctus avec la non publication en 1980 d’un essai qui montrait une forte augmentation de mortalité avec une molécule de cette classe, la lorcainide.
Une étude empirique (« empirical study ») a montré que l’exclusion, dans les méta-analyses des essais non publiés entraîne en moyenne une surestimation de 15% (IC95% 4% ;28%) de la taille de l’effet [4]. De même, l’exclusion des essais publiés uniquement sous forme « d’abstracts » entraîne en moyenne une surestimation de 33% (IC95% 10% ;60%) de l’effet.
La solution à ce problème serait la mise en place de registres prospectifs d'essais qui en enregistrant les essais à leur mise en place, permettraient, par la suite, de retrouver leur trace même s'ils n'ont jamais été publiés.
|
Exemple |
|
Une étude récente publiée
début 2008 dans le New England Journal of Medicine [5] démontre que le biais de publication
(ou plus exactement la publication sélective des essais en fonction de
leur résultat) est encore un problème d’actualité.
L’étude a consistée à
récupérer auprès de la FDA les résultats de tous
les essais de 12 antidépresseurs, soit 74 essais cliniques
déclarés au total. Sur ces 74 essais, 31% (représentant 3449
patients) non pas été publiés. Selon l’analyse
FDA, 38 essais ont obtenus des résultats positifs. Ils ont tous
été publiés à l’exception d’un seul.
A l’exception de 3, les essais considérés par la FDA
comme ayant obtenu des résultats négatifs ou questionnable
n’ont pas été publiés (22 essais) ou ont
été publiés d’uen façon suggérant un
résultat plutôt positif selon l’évaluation des
auteurs (11 essais). En ne regardant que la littérature, 94% des
essais semblent positifs alors que seulement 51% des essais selon
l’analyse FDA ont donné des résultats positifs. |
1 Les registre d’essais
La solution au biais de publication est maintenant apportée par l'impossibilité de publier, dans la majorité des revues, les essais qui n’auraient pas été enregistrés à leur démarrage dans un registre public. Ces registres prospectifs d'essais permettent alors de retrouver la trace de tous les essais entrepris qu'ils soient ou non publiés.
Cette initiative a été prise en septembre 2004 par International Committee of Medical Journal Editors (lien web). Cette association demanda aux journaux de plus publier à partir du 1er juillet 2005 les essais randomisés qui n’aurait pas été déclarés à un registre d’essai lors de leur mise en place. Cette décision permis de solutionner pour tous les nouveaux essais le problème du biais de publication. En effet, à partir de ce moment tout initiateur d’essai ne voulant pas prendre le risque de ne pas pouvoir publier correctement son travail est dans l’obligation d’enregistrer son étude.
Actuellement de nombreux registre d’essais ont été mis en place comme le registre du NIH (www.clinicaltrials.gov), le registre Current Controlled Trials. Un meta-registre est aussi disponible (metaRegister of Controlled Trials).
Dans ce contexte un numéro international standardisé a été proposé, l’ISRCTN. L’OMS a aussi crée son propre registre (the WHO International Clinical Trials Registry Platform). Une liste assez complète des registres existant à travers le monde est disponible à http://www.controlled-trials.com/links/ .
2 Funnel plot
2.1 Principe
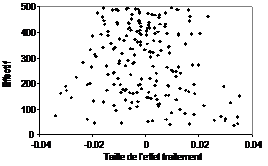
Le graphique dit « funnel plot » (dont une traduction possible est « graphe en entonnoir ») consiste à représenter pour chaque étude la valeur estimée de l’effet traitement en fonction de la taille de son échantillon. En l’absence de biais de publication, les différentes estimations de l’effet du traitement vont se répartir autour de la valeur commune. Les estimations dont l’écart type est important car obtenus dans les études de plus faibles effectifs varieront autour de cette valeur centrale avec une plus grande amplitude que celles dont l’écart type est petit (c’est-à-dire basé sur des plus grands effectifs). Les points se répartissent de façon symétrique de part et d’autre de la valeur centrale et donnent un nuage de points évasé.
Les points situés en bordure de ce
nuage correspondent aux résultats statistiquement significatifs. Avec un
traitement sans efficacité, seul 5% des points sont dans ce cas (Figure 1).
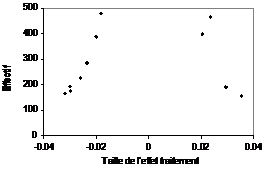
En cas de biais de publication, la répartition n’est plus
homogène. Un déséquilibre apparaît avec disparition
des points situés dans la zone correspondant aux résultats non
significatifs et le graphique devient creux, d’où son nom de
graphique en entonnoir (Figure
2).
Une autre possibilité de biais de publication est
représentée par la non publication des essais allant à
l’encontre de l’hypothèse testée (significatifs ou
non significatifs). Cette possibilité s’avère même
plus fréquente en pratique que
|
Figure 1 – Funnel plot dans une
situation où il n’y a pas de biais de publication |
|
|
Figure 2 – Funnel plot
représentant une situation caricaturale de biais de publication. La
totalité des essais non significatifs n’est pas disponible, ce
qui donne un aspect creux au graphique. |
|
|
Figure 3 – Traduction sur le funnel
plot d’un biais de publication où ce sont les essais
suggérant un effet délétère (significatif ou non)
sont non publiés. |
|
L’analyse graphique du « funnel plot » donne ainsi un moyen de vérifier s’il y a lieu de suspecter un biais de publication dans une méta-analyse.
2.2 Exemples de funnel plot
La figure 4 donne un exemple d’un funnel plot réel très évocateur d’un biais de publication (dans cette méta-analyse, les effets bénéfiques se traduisent par un effect size positif).
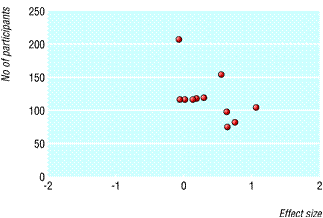
Figure 4 – Funnel plot of randomised controlled
trials comparing topical non-steroidal anti-inflammatory drugs with placebo
(asymmetry P=0.04). Jinying Lin,Weiya Zhang, Adrian Jones, Michael Doherty.
Efficacy of topical non-steroidal anti-inflammatory drugs in the treatment of
osteoarthritis: meta-analysis of randomised controlled trials. BMJ,
doi:10.1136/bmj.38159.639028.7C (published
|
|
|
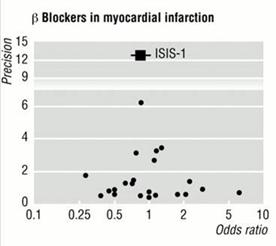
Figure 5 – Exemple de 2 funnel plots permettant d’exclure un biais de publication. En haut du graphique figure le « mega-trial » du domaine.
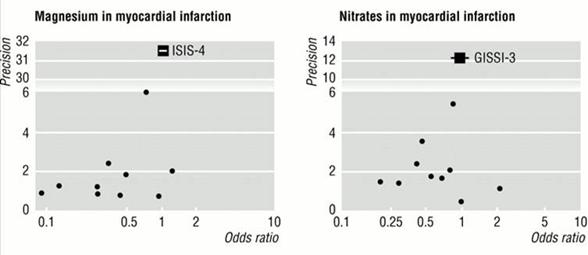
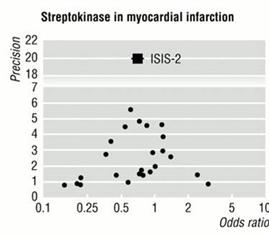
Figure 6 – Exemple de 2 funnel plots évocateur de part leur asymétrie d’un biais de publication. En haut du graphique est représenté le grand essai du domaine montrant l’absence d’efficacité.
3 Bibliographie
1.
Easterbrook PJ, Berlin JA, Gopalan R, Matthews DR. Publication bias in
clinical research. Lancet 1991;337:867-872. PMID:
2.
Dickersin K. The existence of publication bias and risk factors for its
occurrence. JAMA 1990;263:1385-1389. PMID:
3.
Dickersin K, Min Y, Meinert CL. Factors influencing publication of
research results: follow-up of application submitted to two institutional
reviews boards. JAMA 1992;267:374-378. PMID:
4.
McAuley L, Ba'Pham, Tugwell P, Moher D. Does inclusion of gray
literature influence estimates of intervention effectiveness reported in
meta-analysis? Lancet 2000;356:1228-1231. PMID:
5.
Turner EH, Matthews AM, Linardatos E, Tell RA, Rosenthal R. Selective
Publication of Antidepressant Trials and Its Influence on Apparent Efficacy. N
Engl J Med 2008;358(3):252-260. PMID:
Interprétation
des essais cliniques pour la pratique médicale
www.spc.univ-lyon1.fr/polycop
Faculté de Médecine Lyon - Laennec
Mis à jour : aout 2009