Accueil > Sommaire > Statistiques > Intervalle de confiance
1
Introduction
Dans l’interprétation d’un essai thérapeutique, la signification statistique est un élément important qui assure que le résultat obtenu a de forte chance d’être réel et non pas d’être le fruit du hasard. Cependant la signification statistique ne préjuge en rien de l’intérêt clinique du résultat 1.
Signification statistique n’est pas synonyme de signification clinique ou de pertinence clinique
Un test statistique ne se prononce que sur l’existence, probable ou non, d’un effet du traitement, et ne donne aucune information directe sur l’importance de celui-ci. La valeur de p ne représente pas l’intensité de l’efficacité. Un traitement n’est pas d’autant plus efficace que la valeur de p est petite. En effet, toute différence, aussi petite soit-elle, peut-être rendue aussi significative que souhaitée en augmentant le nombre de sujets. Un p significatif peut être obtenu avec un effet dont la taille est cliniquement pertinente, mais aussi avec un effet de petite taille, sans intérêt en pratique, si un très grand nombre de patients a été inclus dans l’essai. Une différence statistiquement significative n’est pas forcément une différence cliniquement significative.
2
Estimation
La pertinence clinique d’un résultat dépend de la taille de l’effet qui est estimé par l’essai thérapeutique. Cette estimation est fournie par la valeur observée dans l’essai (estimation ponctuelle) entourée de son intervalle de confiance (« confidence interval »). L’intervalle de confiance traduit la précision statistique du résultat.
Le but de l’estimation est de déterminer la vraie valeur d’un paramètre, par exemple, la vraie réduction relative de mortalité. Cependant, la valeur estimée dans un échantillon peut être assez loin de la vraie valeur du fait des fluctuations aléatoires d’échantillonnage, c’est-à-dire du fait du hasard. L’intervalle de confiance permet de prendre en compte cette incertitude aléatoire dans la présentation des estimations.
Tout résultat d’essai thérapeutique est
rapporté en mentionnant les valeurs du critère de jugement
observées dans chaque groupe de traitement, l’estimation de la
taille de l’effet entourée de son intervalle de confiance et la
valeur du p du test statistique de l’existence d’un effet non
nul : “A total of 46 patients in the rofecoxib group had a
confirmed thrombotic event during 3059 patient-years of follow-up (1.50 events
per 100 patient-years), as compared with 26 patients in the placebo group
during 3327 patient-years of follow-up (0.78 event per100 patient-years); the
corresponding relative risk was 1.92 (95 percent confidence interval,1.19 to
3
Définition
de l’intervalle de confiance
L'intervalle de
confiance (IC) à 95% est un intervalle de valeurs qui a 95% de chance de
contenir la vraie valeur du paramètre estimé. Avec moins de rigueur, il est possible de
dire que l'IC représente la fourchette de valeurs à
l'intérieur de laquelle nous sommes certains à 95% de trouver la
vraie valeur recherchée. L'intervalle
de confiance est donc l'ensemble des valeurs raisonnablement compatibles avec
le résultat observé (l’estimation ponctuelle). Il donne une
visualisation de l’incertitude de l’estimation.
Des intervalles de
confiance à 99% ou à 90% sont parfois utilisés. La
probabilité (degré de confiance) de ces intervalles de contenir
la vraie valeur est respectivement de 99% et 90%.
L’intervalle de
confiance est constitué des valeurs qui ne sont pas statistiquement
significativement différentes du résultat observé. Les
bornes supérieures et inférieures sont donc les valeurs les plus
éloignées du résultat qui ne lui sont pas statistiquement
différentes. Par contre les valeurs situées à
l’extérieur de l’intervalle sont statistiquement
différentes du résultat observé. Ainsi, la borne
supérieure est la plus grande valeur non significativement
différente de la valeur observée.
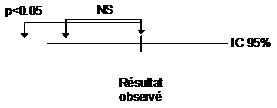

Figure 1 – Interprétation des bornes d’un intervalle de confiance
Exemple
Par exemple (figure 1), une réduction de mortalité de 20% avec un IC 95% de [35% ; 5%] signifie que bien qu’une baisse de 20% ait été observée ponctuellement dans l’essai, il n’est pas possible d’exclure que l’efficacité du traitement soit en réalité plus petite (au pire elle peut être de 5%) ou plus grande (au mieux de 35%).
En d’autre terme, dans cet essai une réduction de 5% n’est pas statistiquement différent de 20%.
1
Relation
entre intervalle de confiance et test statistique
Dans un essai, l'intervalle de confiance visualise la précision avec laquelle l'effet du traitement est connu. La valeur de p est d’interprétation difficile car elle combine à la fois une information sur la taille de l’effet et une sur la précision de l’estimation de la taille de l’effet. Par contre, l’intervalle de confiance présente ces deux informations de manière distincte.
Lorsque l’intervalle de confiance contient la valeur caractéristique de l’effet nul (risque relatif de 1 ou différence de 0), il n’est pas possible d’exclure le fait que la vraie valeur soit cet effet nul. Ainsi la différence observée ne peut pas être considérée comme statistiquement significative.
À l’inverse, un test significatif au seuil de 5% conduit à dire qu’il y a 95% de chance que la vraie valeur de l’effet soit différente de l’effet nul. C’est-à-dire que l’intervalle de confiance à 95% ne contient pas la valeur de l’effet nul.
Ainsi, lorsqu’un test est significatif au seuil a (par exemple 5%), l’intervalle de confiance à 100-a% (c’est-à-dire dans notre exemple 95%) ne contient pas la valeur correspondant à l’absence d’effet (1 pour un risque relatif ou un odds ratio, 0 pour une différence de risque ou de moyenne). À l’opposé, lorsqu’un test n’est pas significatif, l’intervalle de confiance contient cette valeur (figure 2).
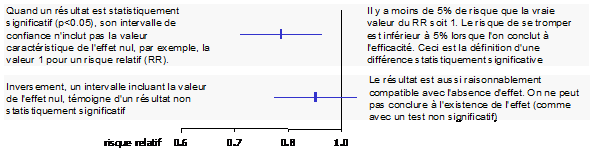
Figure 2 – Correspondance entre intervalle de confiance et test statistique
2
Interprétation
La borne péjorative de l’intervalle de confiance (le plus souvent la borne supérieure) représente le plus petit effet du traitement que l’on ne peut pas raisonnablement exclure.
Les intervalles de confiance permettent de visualiser le plus petit effet du traitement que l’on ne peut pas raisonnablement exclure 2-4. Ce plus petit effet est la borne péjorative de l’intervalle de confiance (borne supérieure le plus souvent quand l’effet est bénéfique).
Cette logique qui cherche à exclure le pire est celle du test statistique. Pour accepter une conclusion d’efficacité du traitement, les données doivent permettre d’exclure avec une « quasi-certitude » (c’est-à-dire avec un risque d’erreur statistique minimal) la survenue du pire (le traitement n’a pas d’effet ou il a un effet délétère). Cette formulation visualise une fois de plus que le seuil classique de 5% est peut être trop élevé vis à vis des interprétations auxquelles il sert de substratum. En effet, peut-on parler de quasi certitude avec un risque d’erreur de 5% ?
2.1
Interprétation
des intervalles de confiance dans le cas d’un résultat
significatif
2.1.1 Premier cas de figure
Dans l’essai A (cf. tableau 1), le traitement entraîne une « réduction » relative du risque (RRR) de -23% (IC95% [-30%,-16%]). Pour cet exemple, une valeur de RRR négative signe une réduction du risque, à l’inverse une valeur positive une augmentation. Cette convention a été adoptée pour mettre sur la partie gauche du graphique les effets correspondant à un effet bénéfique. De ce fait, le graphique des RRR s’interprète de manière similaire à celui des risques relatifs. L’interprétation de ce résultat est qu’il existe un effet statistiquement significatif, de taille importante et connu avec précision. Ce traitement est intéressant en pratique car quelle que soit la valeur réelle de l’effet, celle-ci reste intéressante. Dans le pire des cas, cet effet est encore de -16% ce qui correspond à une réduction relative du risque satisfaisante.
Tableau 1 – Exemple de 5 situations différentes (ces données sont représentées graphiquement sur la Figure 3).
|
Essai |
RRR |
IC 95% |
p |
|
A |
-23% |
[-30%;-16%] |
0,000 |
|
B |
-6% |
[-10% ;-1%] |
0,024 |
|
C |
-23% |
[-41% ;-1%] |
0,043 |
|
D |
0% |
[-4% ;4%] |
1,000 |
|
E |
-19% |
[-48% ;27%] |
0,362 |
|
RRR :
« réduction » relative de risque. Par convention
dans cet exemple, une RRR négative signe une réduction de
risque. A l’opposé, une valeur positive témoigne
d’une augmentation. |
|||

Figure 3 – Exemple d’interprétation de 5 situations différentes (cf. texte)
2.1.2 Deuxième cas de figure
Le traitement dans l’essai B entraîne une « réduction » relative du risque de -6% (IC95% [-10% ; -1%]). L’interprétation de ce résultat est qu’il existe un effet statistiquement significatif, que l’effet du traitement est connu avec précision (l’intervalle de confiance est étroit) mais qu’il n’est pas formellement prouvé que le traitement soit intéressant en pratique. En effet, même dans la meilleure des situations, c’est-à-dire celle où l’effet réel serait proche de la borne inférieure (-10%), la taille de l’effet reste faible et peu intéressante en pratique.
2.1.3 Troisième cas de
figure
Le traitement dans l’essai C entraîne une « réduction » relative du risque de -23% (IC95% [-41% ;-1%]). L’interprétation de ce résultat est qu’il existe un effet statistiquement significatif , la taille de l’effet n’est pas connue avec précision mais il se pourrait que cet effet soit de taille intéressante. En effet, l’estimation ponctuelle (-23%) témoigne d’un effet substantiel de même que la borne inférieure de l’intervalle (-41%). Cependant l’incertitude sur ce résultat est grande, et il est aussi possible que l’effet réel soit quasiment nul (proche de la borne supérieure, -1%). En pratique, il est difficile de recommander l’utilisation de ce traitement car il existe une possibilité qu’il soit peu efficace. Un essai supplémentaire qui permettra d’améliorer la précision de l’estimation de l’effet par une méta-analyse pourrait être souhaitable. Tableau 2 – Exemple de 5 situations différentes (ces données sont représentées graphiquement sur la Figure 3).
2.2
Interprétation
des intervalles de confiance dans le cas d’un résultat
non-significatif
2.2.1 Premier cas de figure
Dans l’essai D, le traitement n’entraîne pas de modification relative du risque (RRR=0%, IC95% de [-4% ;+4%]). Ce résultat n’est pas significatif (p=1,00). Au mieux, il pourrait exister une réduction très faible de 4% qui ne présente pas beaucoup d’intérêt en pratique. Bien qu’en toute rigueur, il ne soit pas possible de conclure à l’absence d’efficacité, l’interprétation de l’intervalle de confiance autorise à conclure que très probablement ce traitement ne serait d’aucune utilité en pratique. Cet exemple montre la supériorité de l’approche par les intervalles de confiance sur celle utilisant uniquement des tests statistiques. En utilisant l’approche des tests statistiques il est impossible de formuler une conclusion (une différence non significative ne permet pas de conclure). Par contre, avec l’approche basée sur les intervalles de confiance et étant donné la précision du résultat, il est licite de conclure à l’absence d’intérêt de ce traitement : même si celui-ci a une efficacité non nulle, la taille de l’effet est trop petite pour être intéressante en pratique.
2.2.2 Deuxième cas de figure
Le traitement dans l’essai E entraîne une « réduction » relative non significative de -19% (IC à 95% de [-48%,+27%]). Il apparaît clairement que ce résultat non significatif n’autorise pas à conclure à l’absence d’effet. En effet, ce résultat est compatible avec une « réduction » relative de -48%, effet de taille conséquente. De plus l’intervalle est en très grande partie du côté favorable ce qui renforce la possibilité de l’existence de l’effet. En conclusion, il est possible que le traitement soit efficace et que cette efficacité soit suffisamment importante pour être intéressante en pratique. Ce résultat encourage à réaliser un nouvel essai de plus grande puissance.
Exemple
La
méta-analyse des essais évaluant
3
Remarques
diverses
3.1
Nécessité
d’essais surpuissants
Pouvoir écarter qu’un traitement possède une efficacité trop petite pour être cliniquement pertinente nécessite d’avoir des intervalles de confiance excluant largement l’absence d’effet. Cette configuration nécessite davantage de puissance que pour simplement exclure l’absence d’effet. En fait le raisonnement devrait être similaire à celui de l’essai de non-infériorité (cf. chapitre Les essais d’équivalence clinique). Il n’est pas suffisant de montrer qu’un traitement a un effet non nul, il conviendrait plutôt de montrer que l’efficacité du traitement est suffisamment importante pour être cliniquement pertinente, c’est-à-dire qu’elle n’est pas inférieure au plus petit bénéfice cliniquement intéressant. Ce point suggère que les essais doivent être surpuissants par rapport à la puissance nécessaire pour rejeter l’absence d’effet. Plusieurs essais ont suivi cette approche. 5-7
3.2
Analyses
intermédiaires
La pratique des analyses intermédiaires se généralise. Elles permettent d’arrêter les essais au plus tôt, dès que le nombre de patients inclus est suffisant pour mettre en évidence l’effet. Ce type d’analyse complique le calcul de l’intervalle de confiance (cf. chapitre Analyses intermédiaires).
Par son principe, ce mode d’analyse conduit, dans les essais arrêtés précocement, à des intervalles de confiance dont la borne supérieure est à la limite de l’absence d’effet. Il devient alors difficile d’analyser si l’effet obtenu est cliniquement pertinent.
Multiplicité des intervalles de confiance et inflation du risque alpha
Un problème d’inflation du risque alpha survient lorsque l’on considère simultanément plusieurs intervalles de confiance, de manière similaire au phénomène survenant lors des comparaisons multiples (cf. chapitre sur les tests statistiques).
Un intervalle de confiance nous assure que si l’on fait le parie que la vraie valeur est comprise entre la borne inférieure et la borne supérieure d’avoir raison dans 95% des cas.
Certaines situations conduisent à s’intéresser simultanément à plusieurs intervalles de confiance. C’est par exemple le cas lorsque l’on décrit l’effet d’un traitement sur tous les critères de jugement mesurés dans l’essai. Ces situations conduisent à une inflation du risque alpha et si l’on fait le pari que toutes les vraies valeurs sont comprises dans leur intervalle de confiance respectif, le risque d’avoir raison n’est plus de 95% mais il est plus faible. D’autant plus faible que le nombre d’intervalle est important. Avec 5 critères, la probabilité que les 5 intervalles de confiances inclus simultanément les 5 vraies valeurs n’est que de 77%.
Pour contrait ce phénomène, il est
possible d’ajuster la largeur des intervalles de confiance à
l’aide de la méthode de Bonferroni, en prenant pour IC à
95% des intervalles en fait à ![]() (où
αaj représente le seuil ajusté par la
méthode de Bonferroni).
(où
αaj représente le seuil ajusté par la
méthode de Bonferroni).
4
Bibliographie
1. Gardner MJ, Altman DG. Confidence intervals rather than P values: estimation rather than hypothesis testing. BMJ Clin Res 1996;292:746-750.
2. Borenstein M. The case for confidence intervals in controlled clinical trials. Controlled Clinical Trials 1994;15:411-428.
3. Rothman KJ, Yankauer A. Confidence intervals vs significance tests: quantitative interpretation. Am J Public Health 1986;75:587-588.
4. Bulpitt CJ. Confidence intervals. Lancet 1987;1:494-497.
5. Collins R, Peto R, Armitage J. The MRC/BHF Heart Protection Study: preliminary results. Int J Clin Pract 2002;56(1):53-6.
6. MRC/BHF Heart Protection Study of cholesterol lowering with simvastatin in 20,536 high-risk individuals: a randomised placebo-controlled trial. Lancet 2002;360(9326):7-22.
7. Pfeffer MA, McMurray J, Leizorovicz A, et al. Valsartan in acute myocardial infarction trial (VALIANT): rationale and design. Am Heart J 2000;140(5):727-50.
Interprétation des essais cliniques pour la pratique
médicale
www.spc.univ-lyon1.fr/polycop
Faculté de Médecine Lyon - Laennec
Mis à jour : aout 2009