Critère de jugement principal et critères de jugements secondaires
Accueil > Sommaire > Critère de jugement principal
1
Généralités
Plusieurs critères de jugement sont souvent envisageables pour mettre en évidence l’effet d’un traitement d’un point de vue clinique. Un effet obtenu au niveau de n’importe lequel de ces critères justifierait l’utilisation de ce traitement en pratique. Cependant si aucune précaution n’est prise, cette multiplicité des critères va conduire à des comparaisons statistiques multiples. En effet, on conclura à l’existence d’un effet du traitement dès lors qu’un des tests statistiques rattachés à ces critères est significatif. Le risque de conclure à tort à l’effet du traitement augmente.
Le moyen le plus simple pour maintenir le risque d’erreur alpha au niveau choisi est de ne faire qu’une seule comparaison. Pour cela, un critère de jugement est privilégié a priori, c’est le critère de jugement principal. La conclusion sur l’efficacité du traitement sera prise uniquement sur cette comparaison. Le risque d’erreur alpha de la conclusion est donc alors parfaitement contrôlé et égal à 5%.
En l’absence de différence significative sur le critère principal, une différence pourtant significative sur l’un ou plusieurs des critères secondaires ne permet pas de conclure. Le risque d’erreur est alors trop grand (Figure 1).
Pour la même raison, la définition du critère de jugement doit préciser le moment de sa mesure. La répétition au cours du temps des comparaisons implique une inflation du risque alpha. L’interprétation des critères de jugement secondaires présente des aspects assez similaires à celle des analyses en sous-groupes (1, 2).
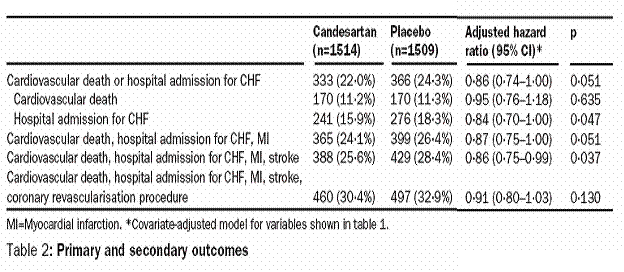
Figure 1 – Exemple de situation où aucune différence significative n’est obtenue au niveau du critère de jugement principal (Cardiovascular death or hospital admission for CHF). Les différences significatives observées au niveau de certains critères de jugement secondaires(Hospital admission for CHD ou Cardiovascular death or hospital admission for CHF, MI, stroke) ne permettent pas d’affirmer l’efficacité du traitement en raison de la multiplication des comparaisons (6 tests au total).
1
Définition
Le critère de jugement principal (« primary endpoint » ou « main endpoint ») est le critère qui va servir à la mise en évidence de l’efficacité du traitement étudié. Il est unique afin de permettre le contrôle du risque de conclure à tort à l’efficacité (erreur statistique alpha). En effet pour éviter les effets pervers de la multiplication des tests statistiques, il convient de ne baser la conclusion de l’essai que sur un et un seul test statistique – celui qui sera fait sur le critère de jugement principal.
Du fait de son unicité, le critère de jugement
doit être soigneusement choisi et doit correspondre au critère le
plus cliniquement pertinent vis-à-vis de l’objectif
thérapeutique de
Parfois, d’autres contingences, moins valides scientifiquement, conduisent à considérer d’autres éléments dans le choix du critère de jugement, comme une fréquence de base plus élevée afin de réduire la taille (et le coût) de l’essai ou une plus grande simplicité d’acquisition.
La réalisation de plusieurs tests statistiques avant de
conclure à l’effet du traitement augmente le risque de faire cette
conclusion à tort. En effet, cette conclusion sera faite dès
qu’un des tests sera significatif. On prend donc un risque d’erreur
de 5% au premier test, puis encore 5% au second, etc. À l’issue de
tous les tests, le risque d’erreur alpha est bien supérieur
à 5%. Avec 5 critères indépendants, la probabilité
de trouver au moins une différence significative à tort est de
23%.
À côté du critère de jugement principal, d’autres critères peuvent aussi être analysés. Ils sont dénommés critères de jugement secondaires (« secondary endpoints »). Ces critères secondaires peuvent être :
· des critères utilisés pour documenter les bénéfices secondaires du traitement (par exemple, si le critère principal est la mortalité totale, le traitement peut aussi réduire la fréquence des événements non mortels, ou augmenter la qualité de vie),
· des critères complémentaires utilisés pour documenter le mécanisme d’action de l’effet obtenu (par exemple, les causes spécifiques de mortalité afin d’expliquer comment est obtenue une réduction de mortalité totale),
· des critères intermédiaires (par exemple le taux de reperfusion coronaire dans les essais de fibrinolyse à la phase aiguë de l’infarctus du myocarde),
· des critères correspondant à des effets délétères du traitement,
· ou les composantes d’un critère de jugement composite utilisé comme critère principal.
Nous verrons cependant dans la section consacrée à l’interprétation, qu’il n’est pas possible de conclure de façon formelle sur un critère de jugement secondaire (même si son analyse été prévue d’emblée dans le protocole). Les critères secondaires sont présents à titre documentaire.
Tableau 1 – Deux exemples de choix de critères principaux et secondaires.
|
|
Exemple 1 |
Exemple 2 |
|
|
Éradication de Helicobacter
pylori dans la dyspepsie |
Antiagrégant
dans la prévention cardiovasculaire |
|
Critère de jugement principal |
Disparition des symptômes de dyspepsie |
Décès + infarctus + AVC |
|
Critères de jugement secondaires |
· Score
de sévérité de la dyspepsie (Glasgow) · Score de qualité de vie · Éradication de H. pylori · Recours à un traitement antisecrétoire |
· Mortalité
totale · Mortalité coronarienne · Mortalité cardiovasculaire · Infarctus mortel et non mortel · Infarctus non mortels · AVC mortel et non mortel · AVC non mortels |
2
Corrélation
entre les critères
Les résultats obtenus au niveau des différents critères d’un essai ne sont pas en général indépendants car il existe une corrélation plus ou moins forte entre les critères de jugement. Par exemple, la mortalité cardiovasculaire est incluse dans la mortalité totale qui sera modifiée si la mortalité cardiovasculaire l’est. Les effets observés sur ces deux mortalités sont donc corrélés. Il en est de même par exemple entre les événements mortels et les événements non mortels. Un traitement qui diminue la fréquence des événements mortels le fait souvent par une diminution de la fréquence des événements mortels et non mortels.
3
Critères
de jugement principaux multiples
Il est parfois nécessaire de prendre plusieurs critères de jugement principaux, en général deux. Dans ce cas l’utilisation d’une méthode statistique, comme la méthode de Bonferroni, est indispensable. Le coût à payer est un plus grand nombre de sujets nécessaires (car le calcul s’effectue avec un alpha plus petit qu’avec un seul test).
Les justifications possibles pour l’utilisation de deux critères de jugement sont :
· la possibilité de démontrer simultanément l’efficacité et la sécurité du traitement, en concluant que le nouveau traitement est supérieur au traitement standard à la fois en efficacité et en sécurité
·
la recherche d’une porte de secours en
aménageant la possibilité de pouvoir conclure sur un
critère moins cliniquement pertinent en cas d’absence de
résultats sur le critère clinique dur. C’est par exemple le
cas d’un essai où le critère le plus intéressant
cliniquement est la mortalité mais où on lui adjoint un
critère morbidité comme critère de secours. En effet, un
bénéfice est en général plus facile à
obtenir sur un critère de morbidité que sur
Exemple
L’essai ValHefT est un essai comparant le valsartan au
placebo dans l’insuffisance cardiaque (3). “The primary outcomes were mortality
and the combined end point of mortality and morbidity, defined as the incidence
of cardiac arrest with resuscitation, hospitalization for heart failure, or
receipt of intravenous inotropic or vasodilator therapy for at least four hours”
Une
méthode statistique appropropriée a été utilisée
pour prendre en compte ce double critère de jugement principal : ”Statistical
analyses were performed at an overall significance level of 0.05, adjusted for
the two primary end points. Each primary end point was tested at a two-sided
significance level of 0.02532, on the basis of the Dunn–Sidak inequality: 
'=1–(1–)1/2”.
Aucune différence significative n’a été observée au niveau de la mortalité, contrairement à ce qui est observé au niveau du 2ème critère principal, le critère composite.
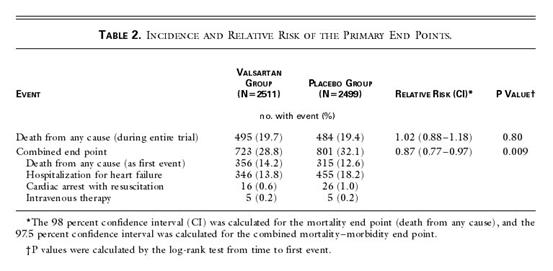
L’existence de ce critère de secours permet finalement de conclure que «Valsartan significantly reduces the combined end point of mortality and morbidity ».
4
Puissance
au niveau des critères de jugements secondaires
La taille d’un essai est déterminée pour garantir la puissance statistique de la comparaison au niveau du critère de jugement principal. Par contre, la puissance de l’essai sur les critères de jugements secondaires n’est pas contrôlée et peut être faible dans certains cas : lorsque la fréquence de base du critère secondaire est inférieure à celle du critère principal ou quand l’effet attendu du traitement est plus petit pour le critère secondaire que pour le critère principal. Ces situations sont courantes. Les événements fréquents sont choisis préférentiellement comme critère principal car ils permettent de réduire la taille de l’essai. Par exemple, un critère composite de morbi-mortalité est plus facilement choisi que la mortalité totale car sa fréquence de base est plus élevée. Ainsi les événements moins fréquents (mais peut être plus cliniquement pertinents) sont envisagés comme critères secondaires mais à leur niveau la puissance et la précision de l’estimation de l’effet seront faibles. Ce point permet de re-insister sur le fait que le critère de jugement principal doit être le critère le plus pertinent et qu’un essai doit être centré sur l’intérêt des patients (choix du critère le plus pertinent cliniquement) et non pas sur celui du traitement (choix du critère permettant d’obtenir le plus facilement un résultat significatif pour le traitement).
Le manque de puissance potentiel sur les critères de jugements secondaires est à prendre en compte dans l’interprétation des résultats.
Ainsi, il n’est pas paradoxal de ne pas mettre en évidence l’effet d’un traitement sur un critère secondaire moins fréquent que le critère principal, alors qu’un effet statistiquement significatif a été observé au niveau de ce dernier. Cette discordance provient simplement du fait que la recherche de l’effet au niveau du critère secondaire manque de puissance statistique et non pas d’un manque d’efficacité du traitement sur ce critère.
De même, les intervalles de confiance obtenus au niveau des critères de jugement secondaires peuvent être plus larges que ceux du critère principal pour la même raison.
Exemple
Dans un essai, 4000 patients ont été nécessaires pour assurer une puissance de 90% à la recherche de l’effet (RR=0,8) sur le critère de jugement principal, dont la fréquence de base était de 20%. Le tableau suivant donne la puissance de la recherche du même effet (RR=0,8) sur des critères secondaires moins fréquents.
|
Critère |
Risque relatif |
Fréquence de base |
Puissance |
|
Critère principal |
0,8 |
20% |
90% |
|
Critère secondaire
1 |
0,8 |
16,5% |
83% |
|
Critère secondaire
2 |
0,8 |
10% |
60% |
|
Critère secondaire
3 |
0,8 |
7,1% |
45% |
|
Critère secondaire
4 |
0,8 |
3,2% |
27% |
5
Prise
en compte de la multiplicité des critères de
jugements secondaires
D’une manière générale, aucune démonstration n’est à attendre au niveau des critères secondaires. Celle-ci est impossible en toute rigueur en raison de l’absence de contrôle strict du risque d’erreur de première espèce et d’hypothèse formulée a priori.
Il est cependant possible de chercher à conclure au niveau des critères secondaires en prenant en compte la multiplicité des tests statistiques résultant de l’analyse des critères de jugements secondaires par une méthode d’ajustement du seuil de signification statistique (4, 5).
5.1
Utilisation
de la méthode de Bonferroni
La méthode de Bonferroni peut être
utilisée pour contrôler l’inflation du risque alpha au
niveau des critères de jugement secondaires. Un seuil ajusté de 
est
utilisé pour chaque critère secondaire (k comparaisons pour
chaque critère secondaire + une comparaison pour le critère
principal), ce qui maintient un risque global d’erreur égal
à a au
niveau de l’ensemble des critères secondaires. L’analyse du
critère principal est effectuée avec un seuil de a.
Cette approche revient à corriger les valeurs de p obtenues au niveau
des critères secondaires en les multipliant par (k+1). Si un
critère secondaire est jugé comme statistiquement significatif
après l’application de ces règles, il est alors possible de
considérer que l’essai démontre l’efficacité
du traitement sur ce critère (1).
Exemple
L’essai SOLVD prevention (6) avait pour objectif d’évaluer si un inhibiteur de l’enzyme de conversion (l’enalapril) pouvait réduire la mortalité des patients porteurs d’une insuffisances cardiaque ventriculaire gauche (IVG) asymptomatique. Six critères secondaires étaient prévus par le protocole : mortalité cardiovasculaire, mort subite, infarctus, AVC, hospitalisation pour insuffisance cardiaque et la qualité de vie. L’essai a inclus 4228 patients qui ont été suivis en moyenne 37 mois.
Le résultat non significatif (p=0,30) obtenu sur la mortalité globale a débouché sur la conclusion qu’il n’y avait pas de preuve que l’enalapril puisse augmenter la survie des patients avec IVG asymptomatique.
Par contre, au niveau des critères secondaires, une réduction significative des hospitalisations pour insuffisance cardiaque (risque relatif de 0,64, p<0,001) ainsi que des infarctus (RR=0,76, p<0,01) était observée.
L’application de la règle d’ajustement requiert que les critères secondaires soient significatifs au seuil de 0,05/7=0,0071. Ainsi il est possible de conclure pour les hospitalisations, mais pas pour l’infarctus.
5.2
Tests
hiérarchisés
Une autre façon de générer la multiplicité des comparaisons au niveau d’un ensemble de critère de jugement est de suivre une procédure de tests hiérarchisés (« hierarchical test procedure », « closed test procedure ») (7). Cette procédure consiste à hiérarchiser, a priori, dans le protocole de l’étude les critères de jugement. Ensuite il est possible de conclure pour tous les critères pour lesquels la signification statistique est obtenue jusqu’au premier non significatif (en descendant dans l’ordre préétabli par la hiérarchie).
Cette procédure permet ainsi de conclure simultanément sur plusieurs critères et autorise ainsi, en toute rigueur, des critères de jugements primaires multiples.
6
Bibliographie
1. Davis
CE. Secondary endpoints can be validly analyzed, even if the primary endpoint
does not provide clear statistical significance. Controlled Clinical Trials
1997;18:557-560.
2. O'Neill
RT. Secondary endpoints cannot be valid analyzed if the primary endpoint does
not demonstrate clear statistical significance. Controlled Clinical Trials
1997;18:550-556.
3. Cohn
JN, Tognoni G. A randomized trial of the angiotensin-receptor blocker valsartan
in chronic heart failure. N Engl J Med 2001;345(23):1667-75.
4. Moye
LA. Alpha calculus in clinical trials: considerations and commentary for the
new millennium. Stat Med 2000;19(6):767-79.
5. Moye
LA. Response to commentaries on 'Alpha calculus in clinical trials:
considerations for the new millennium'. Stat Med 2000;19(6):795-9.
6. The
SOLVD investigators. Effect of enalapril on mortality and the development of heart failure in asymptomatic
patients with reduces left ventricular ejection fraction. NEJM
1992;327:685-691.
7. James J. Chen S-JW. Testing for Treatment Effects on Subsets of Endpoints. Biometrical Journal 2002;44(5):541-557.
Interprétation des essais cliniques pour la pratique
médicale
www.spc.univ-lyon1.fr/polycop
Faculté de Médecine Lyon - Laennec
Mis à jour : aout 2009